An object (suppose it's a baseball, so Fdrag = bv2) is falling through the air. What can we say about its position, velocity, and acceleration as it falls?
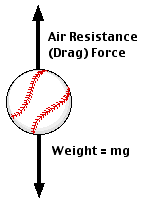 The forces on a falling baseball are shown at right. (Note that if the baseball were moving upward, both its weight and the drag force would be pointing downward, and the net force on the baseball would be different.) The net force on the baseball is, therefore:
The forces on a falling baseball are shown at right. (Note that if the baseball were moving upward, both its weight and the drag force would be pointing downward, and the net force on the baseball would be different.) The net force on the baseball is, therefore:
so the acceleration of the baseball is:
(Equation 1)
Since at terminal velocity:
(where vterm is the object's terminal velocity) we can express the constant b in terms of the object's terminal velocity:
(Equation 2)
Substituting this into Equation 1 gives:
(Equation 3)
You could use either Equation 1 or Equation 3 to calculate the object's acceleration, but Equation 3 is often more convenient since it is generally easier to measure or estimate an object's terminal velocity than it is to measure or estimate the drag coefficient b.
No big deal, right? Well, if you think about how you are going to actually use either of these expressions to calculate the velocity or position of the baseball at some later time it rapidly becomes a big deal. The reason is that the kinematics equations that we know and love (![]() ,
, ![]() , etc.) apply only if the acceleration is constant. The acceleration of the baseball is definitely not constant - it depends on the baseball's velocity, v! What can we do?
, etc.) apply only if the acceleration is constant. The acceleration of the baseball is definitely not constant - it depends on the baseball's velocity, v! What can we do?
We have a problem. The kinematics equations that we know and love are not valid if the acceleration is not constant, but they are the only equations we know! We need to find a way that these equations will be at least approximately correct, but how?
Even though the object's acceleration is changing, if we look at it for a very short time its acceleration doesn't change very much. In other words, if we follow the object for several seconds, its acceleration will change (maybe a lot) and we can't use the kinematics equation ![]() , but if we only follow the object for one-tenth of a second (or so), the acceleration won't change very much and the kinematics equation
, but if we only follow the object for one-tenth of a second (or so), the acceleration won't change very much and the kinematics equation ![]() will be at least approximately correct in this very short time interval. We can then calculate the object's new velocity, at least approximately.
We can use this value as the object's new velocity in this time interval.
will be at least approximately correct in this very short time interval. We can then calculate the object's new velocity, at least approximately.
We can use this value as the object's new velocity in this time interval.
Now that we have the object's velocity during this (very short) time interval we can calculate its displacement during this interval using ![]() . Since the acceleration is approximately constant over a very short time interval, the equation
. Since the acceleration is approximately constant over a very short time interval, the equation ![]() will be approximately true. Therefore the object's new position will be (switching from x's to y's to remind us that we are dealing with vertical position)
will be approximately true. Therefore the object's new position will be (switching from x's to y's to remind us that we are dealing with vertical position) ![]() .
.
Now that we know the object's position and velocity after one very short time interval we can simply repeat the process to find its velocity and position after the next time interval, and so on.
Suppose that a person, intially at rest at x = 0, has a terminal velocity of 60 m/s. Using Equation 3 we can approximate their acceleration at t = 0:
This result is expected, right? Since the velocity of the object relative to the air is zero, the air resistance force on it will be zero. We have known for a long time that if air resistance is not a factor, the acceleration of a falling object is g, right?
Suppose we let 1 second pass. (You may not consider this to be a short time interval, but, hey, I have to calculate this by hand here!) The new velocity of the object will be:
The position of the person at the end of the first time interval is:
Now for the second 1s time interval. The acceleration now will be:
Notice that since the person's velocity has increased, their acceleration has decreased. Their velocity at the end of the second second will be:
The person is moving slightly slower than they would be if there were no air resistance. The position of the person after 2 seconds is:
The person hasn't fallen quite as far as they would have if there were no air resistance.
Now for the third time interval - No wait! This is just dull, repetitive calculation! A computer should be doing this!
last update January 22, 2008 by JL Stanbrough