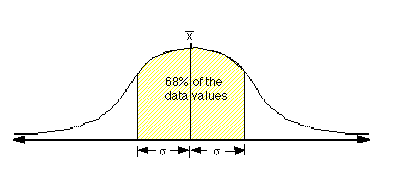
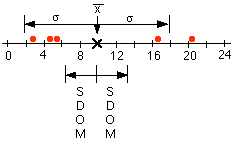
|
In a normal (Gaussian, random) distribution of data,
about two-thirds of the data values will fall within one
standard deviation ( |
 |
|
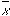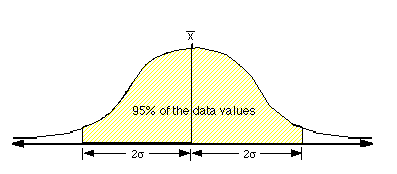
In a normal distribution, about 95% of the data values will fall within two standard deviations of the mean value. |
|
We aren't going to go into the mechanics of calculating the standard deviation of a distribution by hand - you can consult a statistics text if you are interested. You need to know what the standard distribution tells you about your data, and that Excel will calculate it for you using "STDEV(range of cells)".
If your data values are widely dispersed ("all over the place"), then the standard deviation of the data values will be relatively large. This might indicate poor experimental technique (which is bad) or malfunctioning equipment (which is also bad) - in other words, this might be a "back to the drawing board" indicator. On the other hand, if your data values are tightly grouped about a mean value the standard deviation will be a relatively small number.
Actually, what you really want to know is "What is a reasonable uncertainty to assign to the mean value of my data?" - after all, the mean value is the one that you will use as your best estimate. You might suspect at this point that this "reasonable uncertainty" would be either one or two standard deviations (as above), but that isn't exactly true.
Mathematicians have shown that the uncertainty of the mean value
of a normal distribution is smaller - generally much smaller - than
the standard deviation of the entire distribution. (Why is this
reasonable?) They have proven that there is about a 2/3 probability
that the "true value" will lie within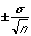 
(where 
is the standard deviation of the data, and n is the number of data
values) of the mean value, and about an 95% probability that the
"true value" will lie within twice this distance from the mean value.
This number ()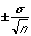
is called the "standard deviation of the mean", and whenever we say
"standard deviation" in reference to a mean value, we mean "standard
deviation of the mean". We will use the standard deviation of the
mean (SDOM) as a measure of the precision of our measurements.
|
Trial |
Group A |
Group B |
|---|---|---|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
Mean Value ( |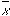
9.8 |
9.8 |
|
Standard Deviation ( |
0.3 |
8.0 |
|
SDOM ( |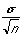
0.1 |
3.6 |
|
Graph |
 |
 |
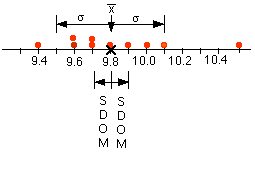
The table above shows some (contrived) data for two ficticious lab groups, Group A and Group B . In this experiment, Group A has run 10 trials for a measurement, and calculated a mean value of 9.8 (in some units). Group B has run 5 trials, and their mean value is also 9.8. Same results, right? Well, no - but we'll discuss that later.
For now, notice that most (but not all) of the data falls within one standard deviation of the mean value, and just about all of the data falls within two standard deviations of the mean. In the example above, only Group A's trial #9 - 10.5 is more than two standard deviations from the mean. This means that it is an unusual value - but unusual things happen all the time!
Group A has not only taken more data (which possibly indicates more time and energy invested) than Group B, but their data values are much more closely grouped, as indicated by the much smaller standard deviation of their data (which possibly indicates more care and skill in gathering the data). Notice, too, that their data produces a much smaller standard deviation of the mean (SDOM), which means that their experiment can provide a much better test
)
)