

The derivative of a function tells you the slope or rate of change of the function. It's a big deal. Here are a few of the ways that the TI-89 can calculate derivatives for you.
Sometimes you are given a function and need to find the derivative of this function. For this, you need to use the TI-89's "d) differentiate" function.
| You can access the differentiation function from the |
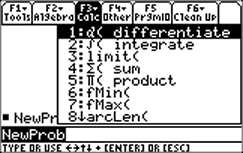 |
| The syntax of the function is "d(function, variable)." For example, if y = x3 - 2x + 4, the derivative of y with respect to x can be found as in the screen shot at right. | 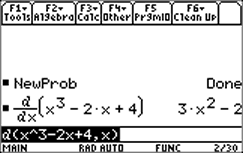 |
| The solution to the problem "If x = 4t2 +1/t, find the derivative of x with respect to t" is shown at right. | 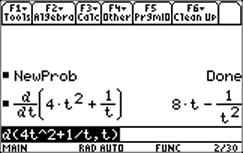 |
Sometimes you just need to know the value of the derivative of a function (the slope of the function's graph) at a particular point. There are a few ways to get this done. Suppose, for instance, that you want to know the slope of the graph of y = 0.4x2 + 1 at the point where x = 3. Here are some methods:
| You could use the "d) differentiate" function along with the "|" operator. A possible advantage of this approach is that this function will try to return an exact value if possible. | 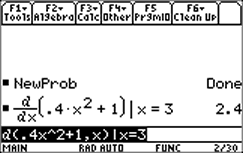 |
| If you graph the function, you can use "6: Derivatives" from the |
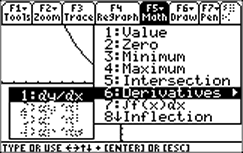 |
| The result of using "6: Derivatives is shown at right. Be aware that the result of this function is always a decimal approximation. | 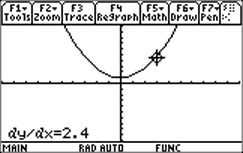 |
| Alternatively, if you graph the function you can use "A: Tangent" from the |
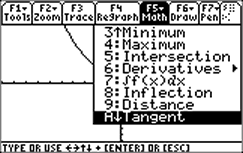 |
| The result of using "A: Tangent" is shown at right. Notice that this function draws the tangent line and gives its (approximate) equation. | 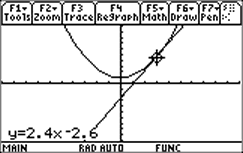 |