

If you read an absolute value statement correctly, the "battle" is almost over.
"Ok, smarty", you might be thinking, "What does |x + 2| mean then? Well, |x + 2| = |x - (-2)|, right, so:
"What about |x|?" you ask? Well, |x| = |x - 0|, so:
Let's solve the inequality "|x - 6| > 3", which is read "the distance from x to 6 is greater than 3".
|
Step 1: draw a number line and label "6". |
|
|
Step 2: Find the points a distance 3 units away from 6. |
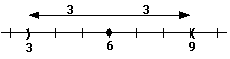 |
|
Step 3: Since x must be farther than 3 units from 6, the shade the portions of the number line where x can be located. Here x < 3 or x > 9. This is the solution to the inequality. |
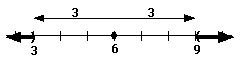 |
Solve the inequality |x + 8| < 4. First, read this statement as "the distance from x to -8 is less than 4".
|
Step 1: Draw a number line and label "-8". |
|
|
Step 2: Find the points a distance 4 units away from -8. |
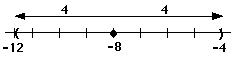 |
|
Step 3: Since x must be closer than 4 units from -8, the shade the portion of the number line where x can be located. Here -12 < x < -4. This is the solution to the inequality. |
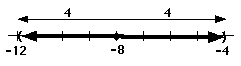 |
Solve the inequality |3x - 6| < 9. First, read this statement as "the distance between 3x and 6 is less than 9".
| Step 1: Draw a number line and label "6". | |
| Step 2: Find the points a distance 9 units away from 6. |  |
| Step 3: From the diagram, -3 < 3x < 15 | |
| Step 4: Solve this simple inequality. | -1 < x < 5 |