![]()
There are a couple of questions that often arise with respect to centripetal force and the rotating Earth:
Everyone (well, almost everyone...) has had the experience of twirling around in a circle and getting dizzy. If you think about this, you will realize that it has to be your rotational velocity that is responsible for this, not your linear (tangential) velocity since you can twirl in place (linear velocity = 0 m/s) and still get dizzy. Suppose you twirl so that it takes 2 seconds for you to complete a revolution (your period, T = 2s). Then your rotational velocity is easily calculated:
If you are just standing still, you are still rotating with the Earth, and your rotational velocity due to the Earth's rotation can also be easily calculated:
The rotational velocity due to the Earth is very, very small compared to your rotational velocity due to spinning around (your spinning-around rotational velocity is about 43,000 times as much in this case!) You are biologically equipped to handle the small rotational velocity due to the Earth - actually, you never even notice it.
This raises a couple more interesting questions (as any good discussion does):
First - is there a difference? Yes, there is. It is possible to tell whether the Earth is rotating and the Universe is standing still, or the Earth is standing still and the Universe is rotating - and it does make a difference. I will tell you that it is the Earth that is rotating, but I'm not going to tell you how I know. A little research will do you good. (Hint: Foucault)
That's easy. Remember that . The rotational velocity of the Earth,
, is very small (4.2 x 10-3 degrees per second), but the radius of the Earth is very large (about 6.37 x 106 meters at the Equator). The rotational velocity looks even smaller when expressed in radians (of course it isn't really smaller!), which is a necessary conversion to use it in
:
This gives:
Of course, this is the linear velocity of someone on the Earth's Equator. How would linear velocity in other latitudes differ? What is your linear velocity at your location on Earth?
| A person standing on a scale at the surface of the Earth |
|---|
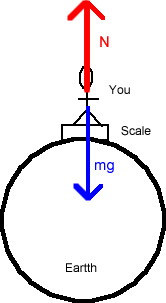 |
Suppose that you are standing on a scale on the surface of the Earth. There are two forces acting on you. The Earth is pulling you downward with a force we call your weight (mg), and the scale is pushing upward on you.
First, suppose that the Earth is not rotating - it (and you) are at rest. Newton's First Law says that the forces on you must balance - the net force on you is zero. Therefore, the scale force equals the weight force - the scale reads your weight, mg.
Now, let the Earth start rotating. You are no longer at rest, you are accelerating. This means that there must be a net force on you - the centripetal force pointing toward the center of the Earth. Therefore, the downward weight force must be greater than the upward scale force, and the difference between the mg force and the scale force equals the centripetal force on you! You weigh less because the Earth is rotating!
How much less? If the Earth is rotating, then if N is the force exerted by the scale:
This says that the scale force (which is what the scale reads) equals your weight minus the centripetal force. So, how much centripetal force is required to keep you rotating with the Earth? Using the previous calculation for your linear velocity at the Earth's surface, and assuming your mass to be 60 kg, you get:
So, your bathroom scale reads about 2 N less (about 0.3% or 1.5 oz) because of the rotation of the Earth.
Also, note that if the Earth were to rotate faster, requiring more centripetal force to keep you moving in a circle, your bathroom scale would read less, since N = mg - Fcent. This is the opposite of what would happen in a rotating space station, isn't it? (Gee! I'm not overweight! The Earth is just rotating too slowly!)
Of course, if the rotation of the Earth increased to the point where the centripetal force needed to make you move in a circle was more than your weight, mg, bad things would happen. What? How long would a day be in this situation?
last update April 21, 2008 by JL Stanbrough