BHS -> Staff -> Mr. Stanbrough -> Physics -> Mechanics -> Kinematics -> this page
An airplane, initially moving at 3.0 m/s down a runway, begins to accelerate down the runway at 3.6 m/s2. How far down the runway will it be in 20 seconds?

vo = 3.0 m/s
a = 3.6 m/s2
= 20 s
= ?
The kinematics equation that relates
, vo, a, and
is:
(Click here to see a derivation.)
substituting:
(Note: A very common blunder is to forget to square the clock reading in the second term!)
Answer: The airplane will be 780 m down the runway in 20 seconds.
This seems like a long way - is it a reasonable answer? Well, suppose that the airplane accelerates at 3 m/s2. In 20 seconds, its velocity will increase by 60 m/s (3*20), so its speedometer will say about 63 m/s. Its average velocity during this time will be about 33 m/s (
= (3 m/s + 63 m/s)/2). If you have an average velocity of 33 m/s for 20 seconds, you will travel about 660 m (distance = average velocity times time.) If the plane's acceleration were 4 m/s2, It's velocity would have increased 4*20 = 80 m/s in 20 seconds, so it would be going 83 m/s, and its average velocity during this time would be (3 m/s + 83 m/s)/2 = 86 m/s/2 = 43 m/s. Since distance equals average velocity times time, it would have traveled 20*43 meters, which is over 800 meters. Yes, our answer is reasonable.
Here is an alternate solution to this problem based on this argument.
A car, initially at rest, begins to accelerate uniformly. If the car travels 1600 m in 12.4 seconds, what was the car's acceleration?Solution:
vo = 0.0 m/s
= 1600 m
= 12.4 s
a = ?
The kinematics equation that relates
, vo, a, and
is:
Solving for a (and keeping in mind that the term containing vo vanishes, since vo = 0 m/s):
Substituting values:
Answer: The acceleration of the car is about 21 m/s2.
This is about 2g's (g = 0.8 m/s2) - is it a reasonable answer? Let's see. Suppose it took 10 seconds to cover the 1600 meters. Since
, the car's average velocity would need to be about 160 m/s to cover 1600 meters in 10 seconds (1600 m/10 s). Now,
, the final velocity of the car would have to be twice the average velocity - about 320 m/s. Now,
, the acceleration would be 320 m/s / 10 s = 32 m/s2. I think our answer is at least "in the ballpark".
How long would it take a rock to fall 20 meters from rest on the Moon, where gmoon = 1.6 m/s2?
= 20 m
vo = 0 m/s
a = gmoon = 1.6 m/s2
= ?
The kinematics equation that relates
, vo, a, and
is:
Solving for
(and keeping in mind that the term containing vo vanishes, since vo = 0 m/s):
substituting
Answer: It would take the rock about 4.0 seconds to fall.
How long would it take a rock to fall 20 meters on the Moon (where gmoon = 1.6 m/s2) if it starts with a downward velocity of 2.0 m/s?
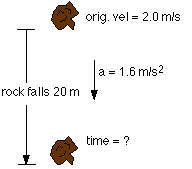
= 20 m
vo = 2.0 m/s
a = gmoon = 1.6 m/s2
= ?
The kinematics equation that relates
, vo, a, and
is:
Although this problem looks a lot like example 7, the vot term does not disappear, which makes this a whole different ball game. What we have is a quadratic equation in
. In some situations you may be able to solve this equation by factoring, but, more likely, you will have to resort to using the quadratic formula:
Substituting and rearranging:
Comparing this equation to the standard-form quadratic shown above, we see that:
substituting into the quadratic formula gives:
Answer: It would take the rock about 3.9 seconds to fall. (Can you figure out what the -6.41 s represents?)