Suppose that you have a mass of 50 kg. Your weight, then is:
W = mg = (50 kg)(10 m/s2) = 500N
Just after you step out of the airplane, the magnitude of your vertical velocity is essentially zero. This means that the air resistance force on you is also zero. After all, since the air resistance force on a person is approximately proportional to the square of the relative velocity - zero velocity means zero force. Since your weight and the air resistance force pull you in opposite directions, the net force on you equals your weight - air resistance:
Fnet = W - AR = 500N - 0N = 500N (down)
Newton's 2nd Law says that your acceleration is:
a = Fnet/m = (500 N)/(50 kg) = 10 m/s2 (down)
So, what's happening to you? Well, you are in free fall, of course. Here I mean physics free fall (falling without air resistance) - not what skydivers call free fall!). Since air resistance is not affecting you, you have a downward acceleration of "g", and your velocity is increasing at about 10 m/s each second - just as if you had jumped off of a chair.

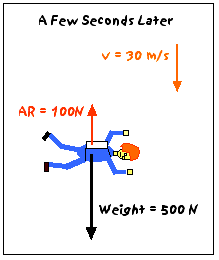
After a few seconds of free fall, you will have a downward velocity of about 30 m/s. Now, there will be an appreciable air resistance force on you - let's say 100 N (up). (Why 100N? It is reasonable and it makes the arithmetic easy.) Now, the net force on you is:
Fnet = W - AR = 500N - 100N = 400N (down)
and Newton's 2nd Law says that your acceleration will be:
a = Fnet /m = (400 N)/(50 kg) = 8 m/s2 (down)
What is happening to you? Well, you are not slowing down - that's for sure! Your acceleration has decreased - not your velocity. You are still speeding up, but you only gain about 8 m/s of speed each second, as compared to 10 m/s each second at the start.
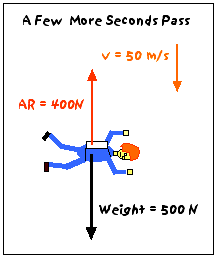
After falling a few more seconds, you have a downward velocity of about 50 m/s. Now, there is considerable air resistance pushing upward on you - let's say 400 N. The net force on you is:
Fnet = W - AR = 500N - 400N = 100N (down)
and your acceleration will be:
a = Fnet /m = (100 N)/(50 kg) = 2 m/s2 (down)
What's going on? Your downward speed is still increasing, but at a much slower rate - you are only gaining 2 m/s of speed each second.
Notice that as you fall, your mass and weight remain constant, but the air resistance force increases. This causes the net force on you to decrease, and if the net force on you decreases, your acceleration decreases.
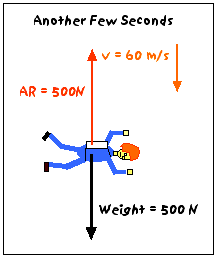
After you fall for another few seconds, you have a downward velocity of about 60 m/s, and the air resistance force on you has increased even more. Let's say it is now 500N.
Fnet = W - AR = 500N - 500N = 0N
Since the net force on you is zero, your acceleration will also be zero (Newton's 1st Law). Now, you are no longer speeding up - you are moving at a constant velocity. This is called your terminal velocity. Unless something happens, this is the velocity that you will have until you hit the ground.
Luckily, you remembered to bring a parachute! When you pull the rip cord and the parachute opens, you (plus the chute) have a much larger surface area than before. Therefore, the air resistance force on you increases drastically. Suppose that the air resistance force is now 2000 N upward. Then:
Fnet = AR - W = 2000N - 500N = 1500N (up)
and according to Newton's 2nd Law, your acceleration is:
a = Fnet/m = (1500 N)/(50 kg) = 30 m/s2 (up)
So, what is happening to you? You have a downward velocity (60 m/s) and an upward acceleration (30 m/s2), so you are slowing down very rapidly - you will lose about half of your speed within one second!
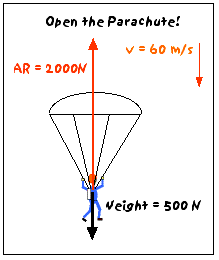
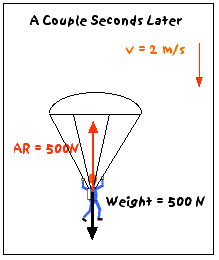
Since you are decelerating so rapidly, it only takes a couple of seconds to reduce your speed drastically. You are now moving downward at about 2 m/s. The air resistance force on you is much less than it was when you were going 60 m/s, but more than just after you jumped out of the airplane, because you ( + parachute) have a much larger surface area. So, suppose that the air resistance force has been reduced to 500 N (upward). Then:
Fnet = W - AR = 500N - 500N = 0N
and, according to Newton's 1st Law, your acceleration must also be zero - you are again moving at a constant velocity, but this constant velocity is low enough that you can land without injury (if you know what you are doing!). Success!