Rainbows

The Angle of Deflection:

The applet below allows you to "experiment" with the interaction of a light ray and a rain drop. The white light ray enters the raindrop on the left. The red and blue portions of this ray are traced through the raindrop. You can move the light ray by clicking and/or dragging your mouse on the left side of the applet.

The table below the rain drop shows the angles of incidence and refraction for each color, as well as the angle of deflection for the ray. (The angle of deflection is the angle between the original direction of the light ray and its direction after striking the rain drop.)

As you move the light ray, observe the effect of the incident angle on the dispersion of the red and blue rays as well as the effect of the angle of incidence on the angle of deflection. (You can find another virtual experiment similar to this one at Circles of Light - The Mathematics of Rainbows.)

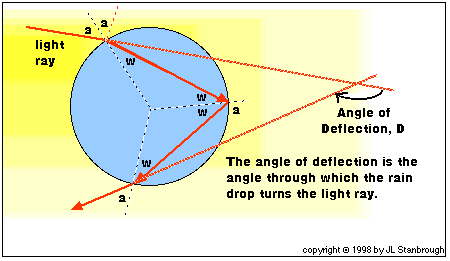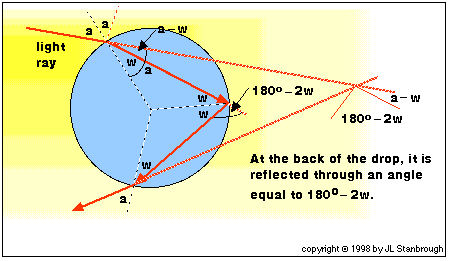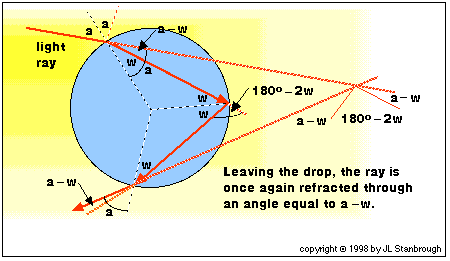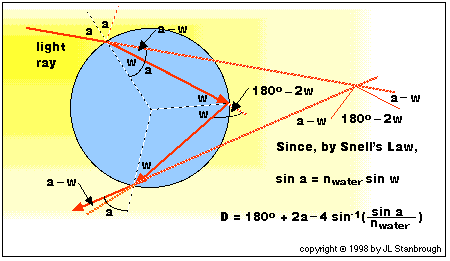
The angle through which the rain drop turns the light ray is called the angle of deflection for the ray. As the diagram below shows, the angle of deflection depends on the angle at which the light ray strikes the drop.

Deflection angle animation

The Rainbow Angle

If you graph angle of deflection vs. angle of incidence (from data collected in a virtual (or real!) experiment, or graph the function derived in the last section, you can clearly see that there is a minimum angle of deflection of approximately 138^o(depending on color). This may ring a bell, since 138^o is the supplement of 42^o, the "rainbow angle" (sometimes called the "Descartes angle"). Why does this minimum value correspond to the angle at which you view a rainbow?

Notice, from the graph, that a fairly-wide range of angles of incidence produce an angle of deflection very near 138^o, so a fairly-large proportion of the incoming sunlight is concentrated in a beam of light leaving the rain drop at about 138^o. For other angles of incidence, the angles of deflection are more spread out.
Notice, from the applet, that larger angles of incidence (near the angle producing the minimum deflection) cause more dispersion of the red and blue rays than small angles of incidence.
The angle at which a light ray strikes a boundary determines the proportion of the ray that is reflected and the proportion that is transmitted. Rays that strike the back of the rain drop at a small angle will reflect a smaller proportion of the ray (more will be transmitted) than rays that strike the back of the raindrop at a larger angle (near the angle that produces the minimum deflection.

Graph animation So, rays that strike the rain drop at an angle of incidence near the angle producing the minimum angle of deflection will tend to form a concentrated, strong beam in which the colors will be widely separated. Rays that strike the rain drop at a small angle of incidence will tend to pass through the drop, and the part of the rays that are reflected inside the drop are spread out relative to one another, while the colors within the rays are not noticeably separated.

What Next?

Well, surely this explains everything there is to know about rainbows! Not so fast, bud. The rainbow is an extremely rich phenomenon, and we have just scratched the surface. There are several couple of features of the rainbow that can be explained by simple ray optics - here are some hints...

Double rainbows are often observed. Where does the second rainbow come from?
- Hint: Part of the light ray remains inside the drop when the light that forms the primary rainbow leaves the rain drop. What is the angle of deflection for the ray that makes a "second lap" around the drop? Is there a rainbow angle for this ray? Does it correspond to the observed angle for the secondary rainbow?
The area of the sky between the the primary and secondary rainbows is noticeably darker than the sky outside the rainbows. Why?
- Hint: Compare the rainbow angles for the primary and secondary rainbows. Are there any angles at which light will not be deflected?
Blue light is refracted through a larger angle than red light, yet the outer margin of the primary rainbow is red, not blue. Why?
The colors observed in the secondary rainbow are reversed from the colors of the primary rainbow. Why?

Have fun!

References:

Circles of Light - The Mathematics of Rainbows - very interesting series of pages on reflection, refraction, and dispersion of light. The mathematics may be intimidating, but everyone should be able to get something valuable from this site.
About Rainbows - Very nicely done - includes demonstrations & experiments you can try, as well as further references.
Physics of Rainbows - features a Java applet that demonstrates the path of a light ray through a spherical drop
Carl B. Boyer, "Kepler's Explanation of the Rainbow", American Journal of Physics 18, 360-366(1950)
Jearl D. Walker, "Multiple Rainbows From a Single Drop of Water and Other Liquids", American Journal of Physics 44, 421-433 (1976)

last update February 10, 1999 by JL Stanbrough