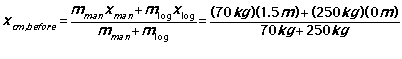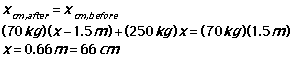Using the Center of Mass
Example: Man Walking on a Floating Log
 A 70-kg man is standing on the end of a 250-kg log that is floating in the water. Both the man and the log are at rest, and the log is 3.0 m long. If the man walks to the other end of the log, how far will the log move in the water? Ignore any forces exerted on the log by the water.
A 70-kg man is standing on the end of a 250-kg log that is floating in the water. Both the man and the log are at rest, and the log is 3.0 m long. If the man walks to the other end of the log, how far will the log move in the water? Ignore any forces exerted on the log by the water.
Solution:
If we take our system to be man + log, no external forces influence our system. Newton's First Law says, then, that if the center of mass was at rest (and it was!) it will stay at rest. Therefore, all we have to do is write an expression for the center of mass of the system before the man moved, and an expression for the system center of mass after the man moved, and set them equal - since the center of mass didn't move.
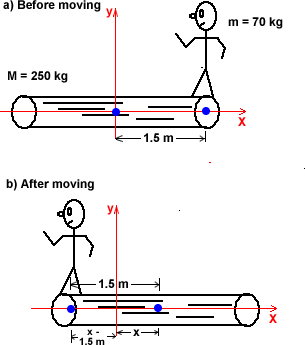
The upper diagram at right shows the starting situation. By symmetry, the center of mass of the log (blue dot) is placed at the center of the log at the origin. The center of mass of the man + log system is now easy to calculate:
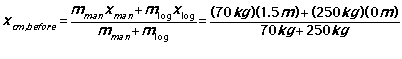
The lower diagram at right shows the ending situation. Since the man has moved to the left, the log has moved a distance x to the right. This puts the man at position x - 1.5 m. The center of mass in this situation is:
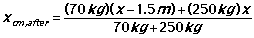
Since the center of mass of the system didn't move, you can say:
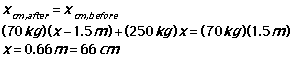
The log moved 66 cm to the right.
last update March 14, 2006 by JL Stanbrough
 A 70-kg man is standing on the end of a 250-kg log that is floating in the water. Both the man and the log are at rest, and the log is 3.0 m long. If the man walks to the other end of the log, how far will the log move in the water? Ignore any forces exerted on the log by the water.
A 70-kg man is standing on the end of a 250-kg log that is floating in the water. Both the man and the log are at rest, and the log is 3.0 m long. If the man walks to the other end of the log, how far will the log move in the water? Ignore any forces exerted on the log by the water.