AP Physics
Simulating Inelastic Collisions
![[Next]](../../../NavIcons/Next.GIF)
![[Home]](../../../NavIcons/Home.GIF)
![[Help]](../../../NavIcons/Help.GIF) [Lab Index]
[Lab Index]
Introduction:
The Interactive Physics™ program makes it easy
to simulate inelastic collisions between objects of various masses
with various velocities. In addition, the software makes it possible
to switch reference frames quickly and easily.
In particular, collisions turn out to be very interesting (and
simple!) when viewed from the center of mass, or as a physicist would
say, in the center of mass frame of reference. When you finish this
simulation you should be able to tell:
- How does the center of mass of a system move during an
inelastic collision? Why does it do that?
- How do the colliding objects move relative to the center of
mass during a one-dimensional inelastic collision?
- How do the colliding objects move relative to the center of
mass during a two-dimensional inelastic collision?
Part 1 - The Earth Frame of Reference:
Setup:
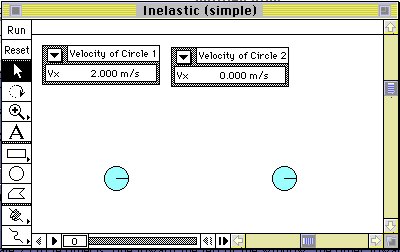 Open the
Interactive Physics program.
Open the
Interactive Physics program.
- Create 2 circle (or square) objects, one toward the left of
the window, the other toward the right side of the window (as
shown).
- Set Gravity to "None" (World menu).
- Open the properties window (Window menu), and:
- give each object a mass of 1.0 kg,
- give each object an elasticity of 0.00
- give one object a velocity (vx) of 2.0 m/s
toward the other. Leave the second object at rest.
- Attach a "meter" to each object to measure the x-component of
its velocity (vx).
- Select "X Graph" from the Velocity sub menu in the
Measure menu.
- Select "Digital" from the pop up menu on the upper-left
corner of the meter.
Run the Simulation:
Run the simulation for various values of the masses, and various
initial velocities. Do the results correspond to your theoretical
predictions?
Part 2 - The Center of Mass
Setup:
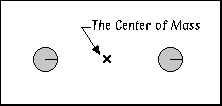 Select
"System Center of Mass" from the View menu.
Select
"System Center of Mass" from the View menu.
Run the Simulation:
When you run the simulation, the center of mass of the system will
appear as a bold "X" in the window. Study the motion of the center of
mass of the system for several collisions. What can you conclude
about the motion of the center of mass before and after the
collision? Turn on "Tracking." Discuss the reasonableness of your
findings.
Part 3 - The Center of Mass Frame of Reference
Setup:
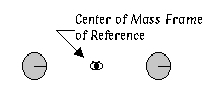 Select the
center of mass with the mouse, and choose "New Reference Frame"
from the View menu to establish a "System Center of Mass"
reference frame.
Select the
center of mass with the mouse, and choose "New Reference Frame"
from the View menu to establish a "System Center of Mass"
reference frame.
- Be sure that the center of mass reference frame is selected as
the current reference frame (at the bottom of the View menu).
Run the Simulation:
Run the simulation using several different masses and initial
velocities. Viewed from the center of mass of the system, how do
these motions appear? Why?
Part 4 - Two-Dimensional Inelastic Collisions
Setup:
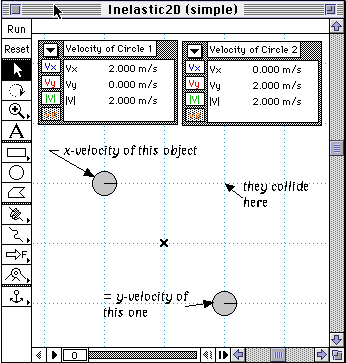 Delete your
velocity meters, and replace them with meters to measure the
two-dimensional velocity (All).
Delete your
velocity meters, and replace them with meters to measure the
two-dimensional velocity (All).
- A difficulty with two-dimensional collisions is that the
objects can easily miss each other. To avoid this, turn on
"GridLines" in the Workspace sub menu of the View menu. This will
allow you to align your objects for a collision. For instance,
since the objects at right have equal speeds, they are positioned
at equal distances from the collision point. If one object had
twice the speed of the other, position it twice as far from the
collision point.
Run the Simulation:
Run the simulation using different masses and velocities. Be sure
to view each collision from both reference frames (Earth and center
of mass). What can you conclude?
![[Next]](../../../NavIcons/Next.GIF)
![[Home]](../../../NavIcons/Home.GIF)
![[Help]](../../../NavIcons/Help.GIF) [Lab Index]
[Lab Index]
last update November 26, 2007 by
Jerry L. Stanbrough