 It is an easy, straightforward problem to find the velocity of the center of mass of the two-car system immediately after the collision. First, the x- and y-components of the velocity of the center of mass:
It is an easy, straightforward problem to find the velocity of the center of mass of the two-car system immediately after the collision. First, the x- and y-components of the velocity of the center of mass:Two cars approach an intersection at a 90o angle and collide inelastically, sticking together after the collision. What is the velocity (speed and direction) of the two-car clump of twisted metal immediately after the collision?
Sounds like this could develop into a complicated problem, doesn't it? Well, there's good news. It isn't a complicated problem, because the velocity of the cars after the collision has to be the same as the velocity of the center of mass of the two-car system immediately before the collision. In other words, a two-dimensional inelastic collision solves exactly like a one-dimensional inelastic collision, except for one additional easy calculation. Viewed from the center of mass, all inelastic collisions look alike!
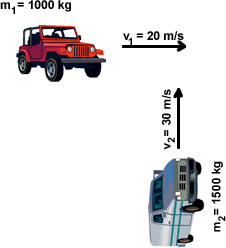
A 1000 kg car is moving eastward at 20 m/s. It collides inelastically with a 1500 kg van traveling northward at 30 m/s. What is the velocity of the two vehicles immediately after the collision?
 It is an easy, straightforward problem to find the velocity of the center of mass of the two-car system immediately after the collision. First, the x- and y-components of the velocity of the center of mass:
It is an easy, straightforward problem to find the velocity of the center of mass of the two-car system immediately after the collision. First, the x- and y-components of the velocity of the center of mass:
knowing the x- (eastward) and y- (northward) components of the velocity of the center of mass, the magnitude is:
Also, the angle that the velocity vector makes with the x- (eastward) axis is a routine calculation:
Since the velocity of the system's center of mass is unaltered by the collision, the two vehicles have a velocity of 19.7 m/s at an angle of 66o north of east immediately after the collision.
last update March 13, 2006 by JL Stanbrough