Calculating with Powers
Suppose you make a measurement, x, whose absolute
uncertainty is .
What will be the uncertainty in p, if p =
x2? Since p = (x)(x), the product
rule applies, and the relative
uncertainty in p will be twice the relative
uncertainty in x.
This idea can be easily extended for any power, n:
The relative uncertainty in xn is n times the relative uncertainty in x.
For example, suppose that the side, s, of a cube
measures.
(This is a 0.5 % measurement.) What is the volume of the cube?
Certainly the volume V = s3, so the best estimate for V =
(20.0 cm)3 = 8.00 x 103 cm3. The
relative uncertainty in V is 3 times the relative uncertainty in s =
3(0.5%) =1.5%. The volume of the cube is, therefore:
Suppose that ,
and that x has a value of 100 with a relative uncertainty of 2% (and
some units). What will be the uncertainty in p? Well, the power rule
applies here - the square root is equivalent to the one-half power.
The value of p will be
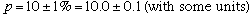
The relative error inis (relative error in x) divided by n
I hope that you noticed that whenever you do arithmetic with measurements, the precision of the result always seems to be less - often alarmingly less - than the precision of the original measurements. Is there ever a situation in which the precision increases? Well, yes and no.
Remember that counts and pure numbers are assumed to be absolutely
precise - that is, if you count 10 periods of a pendulum, 10 is
considered to be exact, not 10 plus or minus
anything. Suppose that you measure the time for 10 periods of a
pendulum as ,
what is the time for 1 period? It is
!
Why is the absolute uncertainty also divided by 10? Since 10 is an
exact value, both the original time measurement and the resulting
period measurement will have the same relative
uncertainty (1.6%).
If k is an exact value, and x is a measurement, the relative error of kx or x/k is the same as the relative error of x.
When you calculate with measurements, you either add absolutte or relative uncertainties to obtain the precision of the result. What this means for the planning of experiments is that: