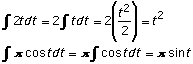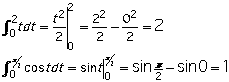Calculus for AP Physics

Introduction:

AP Physics C is a calculus-based physics course, but the fact is that you can do pretty well, grade-wise, in AP Physics C - particularly the mechanics part - without any knowledge of calculus. Of course it won't hurt you to know what is going on with all those strange mathematical symbols and concepts, and there will definitely be problems on the AP Test that require a knowledge of calculus. Fortunately, you can get by really well - even on the AP Test - with very rudimentary calculus skills that can be learned in a few minutes.

You need to know something about:

Derivatives - a derivative is a rate of change, or graphically, the slope of the tangent line to a graph. Although physics is "chock full" of applications of the derivative, you need to be able to calculate only very simple derivatives in this course.
Definite Integrals - a definite integral represents an area, and there are a myriad of applications of integrals in physics. In this course, you need to be able to evaluate only very elementary integrals.

Derivatives:

A derivative is a rate of change, which, geometrically, is the slope of a graph. In physics, velocity is the rate of change of position, so mathematically velocity is the derivative of position. Acceleration is the rate of change of velocity, so acceleration is the derivative of velocity. Net force is the rate of change of momentum, so the derivative of an object's momentum tells you the net force on the object. These are only a few of the applications of the derivative in physics.

Derivative Rules:

Finding the derivative of a function ("differentiating" in calculus language) is a rule-based operation. In other words, you need to recognize what derivative rule applies, and then apply it. In order to recognize what derivative rule applies, you need to know some derivative rules. The tables below list the derivative rules that you will use in this course, and shows some examples of their use. These rules are stated using "t" as a variable (the derivative is "with respect to" t, in calculus language), since most of the functions that we will use are functions of time. If you are taking a derivative whose variable is "s," simply substitute "x" for "t" in the derivative rule.

Rules for Particular Functions:

Rule in English	Rule in Math. Notation	Example
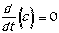
The derivative of a constant is zero.		If x(t) = 5, then v(t) = 0. If v(t) = -3, then a(t) = 0.
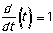
The derivative of t is one.		If x(t) = t, then v(t) = 1.
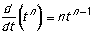
The derivative of t to a power is the power times t to the "one less" power.		If x(t) = t², then v(t) = 2t¹ = 2t. (n = 2) If v(t) = t⁴, then a(t) = 4t³. (n = 4) If x(t) = t^-3, then v(t) = -3t^-4. (n = -3)
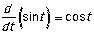
The derivative of the sine of t is the cosine of t.		If x(t) = sin t, then v(t) = cos t.
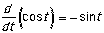
The derivative of the cosine of t is the negative of the sine of t.		If v(t) = cos t, then a(t) = -sin t.

Rules for Combinations of Functions: In the rules below, u and w represent functions of time, t.

Rule in English	Rule in Math. Notation	Example
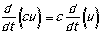
The derivative of a constant times a function equals the constant times the derivative of the function.		If x(t) = 3t², then v(t) = 3(2t¹) = 6t. (c = 3 and u = t²) If v(t) = 4sin t, then a(t) = 4cos t. (c = 4, u = sin t)
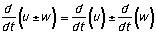
The derivative of the sum (or difference)of two functions is the sum (or difference) of their derivatives.		If x(t) = t + sin t, then v(t) = 1 + cos t. (u = t, w = sin t) If v(t) = t² - 4t, then a(t) = 2t¹ - 4(1) = 2t - 4. (u = t², w = 4t)
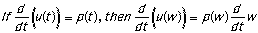
The derivative of a composite (one function inside another function) function equals the derivative of the "outside" function leaving the "inside" function alone, times the derivative of the "inside" function. (The Chain Rule)		If x(t) = (t + 2)², then v(t) = 2(t + 2)¹(1 + 0) = 2(t + 2). (u = t², w = t + 2) If v(t) = sin(2t³), then a(t) = cos(2t³)(2)(3t²) = 6t²cos(2t³) (u = cos t, w = 2t³)

Rule in English

Rule in Math. Notation

Example

The derivative of a constant times a function equals the constant times the derivative of the function.

If x(t) = 3t², then v(t) = 3(2t¹) = 6t. (c = 3 and u = t²)

If v(t) = 4sin t, then a(t) = 4cos t. (c = 4, u = sin t)

The derivative of the sum (or difference)of two functions is the sum (or difference) of their derivatives.

If x(t) = t + sin t, then v(t) = 1 + cos t. (u = t, w = sin t)

If v(t) = t² - 4t, then a(t) = 2t¹ - 4(1) = 2t - 4. (u = t², w = 4t)

The derivative of a composite (one function inside another function) function equals the derivative of the "outside" function leaving the "inside" function alone, times the derivative of the "inside" function. (The Chain Rule)

If x(t) = (t + 2)², then v(t) = 2(t + 2)¹(1 + 0) = 2(t + 2). (u = t², w = t + 2)

If v(t) = sin(2t³), then a(t) = cos(2t³)(2)(3t²) = 6t²cos(2t³) (u = cos t, w = 2t³)

Definite Integrals:

A definite integral represents an area, and evaluating a definite integral ("integrating" in calculus language) is the inverse of finding a derivative - like subtraction is the inverse of addition. In physics, the area under a velocity vs. time graph represents displacement, so the definite integral of velocity gives displacement. The area under an acceleration vs. time graph equals change in velocity, so the definite integral of acceleration tells you the change in velocity. The area under a force vs. position graph equals work done by the force, so the definite integral of force (with respect to position) tells you the work done by the force. There are many, many more applications of the definite integral in physics.

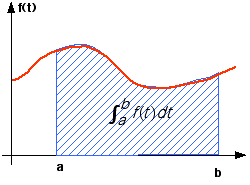
area as an integral

The diagram above shows the relationship between the definite integral notation and the area it represents. "a" and "b" - called "limits of integration" go at the bottom and top of the big "S". "f(t)" is the function being integrated (the "integrand"), and "dt" says that "t" is the variable being used.

The notation is read "the definite integral from a to b of f of t, dt".

Rules for Definite Integrals:

Just like you can subtract 5 from 12 by thinking, "What do I have to add to 5 to get 12?", you can evaluate definite integrals by thinking "What function would I have to differentiate to get the function in this integral?" That function is called the "integral" or "antiderivative." The mathematical symbol for the antiderivative looks like the definite integral without the limits of integration.

Antiderivative Rules for Particular Functions: If you are a calculus student, you will notice that we are ignoring an important mathematical point in the following rules.

Rule in English	Rule in Math. Notation	Example
The antiderivative of a constant is the constant times t.
The antiderivative of t to a power is t to the power-plus-one, divided by the power plus one.	(This is the inverse of the derivative formula )
The antiderivative of the sine of t is the negative of cosine t.	(This is the inverse of the derivative formula .)
The antiderivative of the cosine of t is the sine of t.	(This is the inverse of the derivative formula .)

Antiderivative Rules for Combinations of Functions: In the rules below, u and w represent functions of time, t.

Rule in English	Rule in Math. Notation	Example
The antiderivative of a constant times a function equals the constant times the antiderivative of the function.
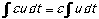
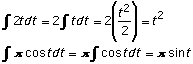
The antiderivative of the sum (or difference) of two functions equals the sum (or difference) of their antiderivatives.

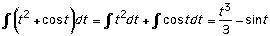
The Fundamental Theorem of Calculus - tells you how to evaluate definite integrals based on what you know about antiderivatives.

Rule In English	Rule in Math. Notation	Example
If F(t) is an antiderivative of f(t), then the definite integral from a to b of f equals the function F evaluated when t equals b minus F evaluated when t equals a.

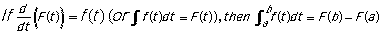
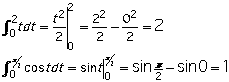
last update November 26, 2007 by JL Stanbrough