![]()
It would seem (to the uninitiated) that determining if a particular motion is motion with constant acceleration would be a straightforward job. Use a motion detector and look at the graph of acceleration versus time produced by the computer software. Is the graph a horizontal line, or not?
However, it isn't quite so easy in the real world. The motion detector calculates the distance to the object by timing pulses reflected from the object and knowing (hopefully) the speed of the pulses: d = vt/2. Any small discrepancy in timing or reflection will produce a small spike in the position versus time graph, but that usually is not a big problem. The velocity of the object is calculated by the software based on the time between successive positions, so small errors in position are magnified into very noticeable errors in velocity. The velocity versus time graphs produced by motion detector software are often, if not usually, irritatingly irregular. The acceleration of the object is calculated from the velocity calculations, and very noticeable irregularities in the velocity produce ridiculous irregularities in the acceleration - so much so that the acceleration versus time graphs produced by motion detector software are generally unusable. So, much like the party game where the first person whispers something to the person next to them, and so on, what comes out at the end often bears no resemblance to the original message.
Another problem with using software-generated velocity versus time graphs and acceleration versus time graphs is that the calculations that are made on the original data are hidden. How do we know what goes on deep in the bowels of the software? Therefore, it is a good idea to stick to position versus time data and ignore the rest.
So, how do you tell if a motion is motion with constant acceleration, then? Well, if an object moves with constant acceleration, then its motion is described by the kinematics equation
and in particular, if the object starts from rest, vi =0, so:
.
So, the test for constant acceleration from rest could be "is the displacement of the object proportional to t2?" Fortunately, this question is easy to answer from position versus time data.
In this lab, you will examine several motions and determine if they are motion with constant acceleration. The motions are:
| Pasco ScienceWorkshopTM 500 Interface (CI-6760) | Pasco USB/Serial Converter (CI-6759) | Pasco Motion Sensor II (003-06758) |
| Pasco Collision Cart (ME-9454) | Pasco 2.2-meter Dynamics Track | pulley |
| set of hooked masses | coffee filters | c-clamp |
| ring stand | right angle clamp | basketball |
| string | ring-stand adapter for motion detector | bumper for dynamics track |
| The pulley attaches to the end of the dynamics track. You need to stop the timer before the weight hits the floor. | 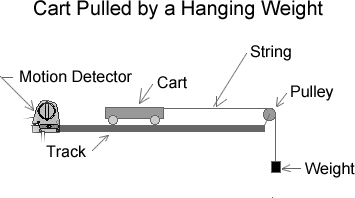 |
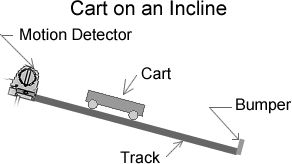
Prop up one end of the dynamics track at a shallow angle, and attach a bumper to the other end. Catch the cart before it hits the bumper - the bumper is a "last resort." What happens if you give the cart an initial velocity up the incline? |
 |
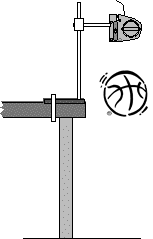
Attach the motion detector a ring stand, and c-clamp the ring stand to the lab table. You should be able to record at least two or three bounces of the basketball. Note: The entire motion is certainly NOT motion with constant acceleration, since the ball obviously undergoes very large upward accelerations when it contacts the floor that are not present when it is in the air. Therefore, the question is: "Does the ball have a constant acceleration while it is in the air?" |
 |
| Place the motion detector on the floor, and orient it so that it detects vertical motion. Drop the coffee filter from directly above the motion detector. If a breeze blows the filter off course, add a few more coffee filters. | 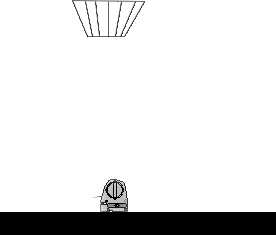 |
last update September 10, 2006 by JL Stanbrough