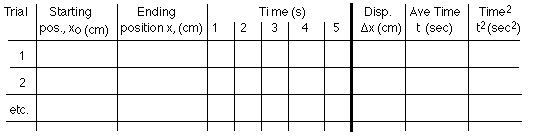AP Physics - Experiment 3a

Motion on an Inclined Plane (Galileo's Experiment)

(Low-tech version... sort of...)

BHS -> Staff -> Mr. Stanbrough -> AP Physics-> AP Labs-> this page

---

Purpose:

Is the free-fall acceleration at the surface of the Earth ("g") constant, and if so, what is its value?

---

Discussion:

Around 1600, the amazing Galileo Galilei was able to show, experimentally, not only that the acceleration of objects in free fall was constant, but was able to determine a pretty good value for this acceleration. Galileo performed this feat by rolling wooden balls down long inclined planes, and he didn't even have the luxury of a clock!

Today, we have the laboratory luxuries like air tracks, stopwatches - even photogate timers! Surely we can do as well as old Galileo...

Theoretically, we know that if an object starts from rest and accelerates at a uniform rate, the distance that it travels in time t is given by:

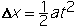
Therefore, if the acceleration of an object is constant, the graph of 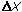vs. t² will be a straight line, with slope equal to half the acceleration. This will answer the question of whether the acceleration is constant or not, as well as provide a value of the acceleration (if it is constant) - but how do you get from there to a value of "g"?

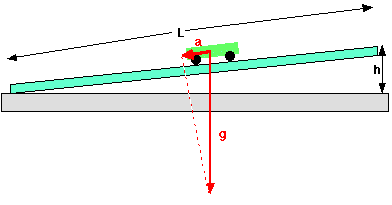
Look at the diagram above. L is the length of the incline, h is the height of the elevated end. The acceleration of the cart , a, acts along the incline, while the free-fall acceleration, g, acts straight down. From similar triangles:

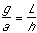
or:

---

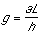
Equipment:

air track & glider	meter stick or measuring tape	stopwatch or photogate timer
vernier caliper	carpenter's level	index card
small blocks or notebooks to prop up one end of the air track

---

Setup:

1. Construct a data table. You will be measuring several distances along the air track (starting position and ending position, actually) and the time that it takes the glider to cover each distance. In order to establish the uncertainty of the time measurement, it will be a good idea to run at least a few trials for each distance. Then, you can calculate and use the average time as the time for this distance. A heading for a sample data table is shown below:
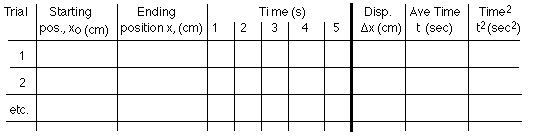
2. Use a carpenter's level to level the air track. The glider should move with a relatively constant velocity when you give it a push, and should stay where you put it.
3. Now, raise one end of the air track by placing a small block of wood or a notebook under one end. The air track glider should now accelerate slightly down the incline. The thickness of this block is the height h in the equations given above. Measure this distance, h, with a vernier caliper. Record your results, along with a precision estimate.
4. Measure and record the distance L along the air track. Don't forget precision.
5. If you are using a photogate timer, place the "main" photogate at the starting point on the air track and the other 10 cm to 20 cm further down the track. Set the timer to record the time for the glider to pass between the photogates (pulse mode). You may need to construct a simple "flag" from an index card to trip the photogates reliably.

		The photogate timer's "control panel" set on pulse mode.

---

Procedure Hints:

1. When you "launch" the glider, be sure that you don't give it a push - either up or down the track.
2. You can keep the same starting position for every trial and increment the ending position 10 cm to 20 cm per trial.
3. After you have timed the glider over as wide a range of distances as possible, find some other blocks that will give the air track a few different angles.  

---

Results:

1. Calculate displacement, average time, and time squared for each trial.
2. Construct a displacement vs. time squared graph for each air-track angle. Be sure to draw the best smooth curve through the data points.
3. If the best smooth curve happens to be a straight line, calculate the slope of the line, and the acceleration of the glider. Be sure to show a clear, organized sample calculation. Don't forget precision.
4. Calculate "g" for each air-track angle. Show a sample calculation. You might as well calculate an "average g", also. What is the precision estimate for this calculation?

---

Conclusions:

So, is the free-fall acceleration at the surface of the Earth ("g") constant, and if so, what is its value?

1. How confident can you be in your results? Why do you think so?
2. What measurement contributed the most uncertainty to your results? What could be done to improve it?

BHS -> Staff -> Mr. Stanbrough -> AP Physics-> AP Labs-> this page