Physics Lab

Measuring "g" - Time of Fall Method

(uses a Pasco Interface)

BHS -> Staff -> Mr. Stanbrough -> AP Physics-> Kinematics-> this page

---

Purpose:

To measure the acceleration of free fall, "g".

---

Discussion:

The kinematics of constant acceleration tells us that:

so, as long as air resistance is not a factor, if you drop an object from rest from a relatively height, h:

where t is the time that it takes to fall the distance h. Solving for g gives:

Therefore, it is theoretically straightforward to determine the acceleration of free fall simply by dropping something and measuring the time it takes to hit the ground.

Experimentally, however, it is exceedingly difficult to get precise-enough times for meaningful results. (It often turns out that the theoretically straightforward approach is exceedingly impractical in the "real world"...) Over short distances (and short times), human reaction time destroys the precision of the measurement, and over long distances, air resistance becomes a factor so that the acceleration of the object is no longer constant and the calculation is invalid. These considerations (among others) are what forced Galileo to develop his famous inclined plane experiment.

The Pasco Free-Fall Adapter gives us the technology to obtain precision timing for objects dropped relatively short distances, however. When the ball is dropped, it activates a switch to start a very accurate timer. When the ball strikes the pad at the end of its fall, it trips another switch to stop the timer. Simple and straightforward!

---

Equipment:

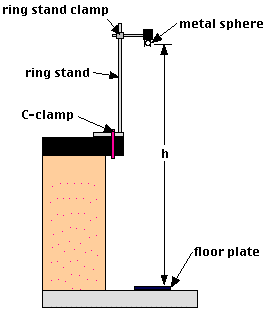
Pasco Science WorkshopTM interface	free-fall Adapter
meter stick/metric tape	metal sphere
ring stand	ring stand clamp
C-clamp

---

Setting Up:

Set up the apparatus as shown in the diagram above. The C-clamp just needs to be tight enough to keep the apparatus from being knocked off the lab table - demonstrate you monstrous strength elsewhere, please.

Setting Up the Pasco Interface:

---

Hint:

Turn on "Show Balloons" in the Help Menu. It will explain the purpose of the various icons in the Pasco interface - which is a big help.

---

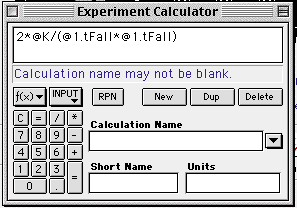
1. Here is what the Calculator Window might look like for a calculation of acceleration. You should understand how this formula relates to the equation shown above.

   Hook up and initialize the Pasco Science Workshop^TM interface.
2. Set up the free fall adapter () to measure the time of fall for the sphere.
3. Enable keyboard entry () for the height of fall.
4. Although the Science Workshop^TM supplies an automatic calculation of acceleration (and I'm sure that it's very nice of them to do so) we are not going to use it. (No "magic boxes, remember?) It is convenient to have acceleration calculated for each trial, however, in order to tell if everything is working reasonably, so you can make your own calculation for acceleration.
5. Create a data table () to display time of fall, height, and acceleration.
6. Create a graph () to display time of fall vs. height.
   1. Open the Graph Setup dialog (), and uncheck "Connect Points". You can also enable point protectors if you wish.
7. Resize and arrange the windows for a convenient display.
   

---

Procedure:

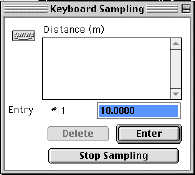
I'm not sure what the Pasco people have in mind for this lab, but the following procedure seems to work pretty well. Of course, if you have a better idea, try it! Basically, each "run" consists of several trials at the same height. I've found that adjusting the height during a run leads to problems (like the ball missing the floor switch...). This also allows you to get a good idea of the timing precision. A Science Workshop^TM graph window will only display three data runs at once, but you can transfer the averaged data to Graphical Analysis^TM for analysis. Here's how:

1. Line up the free-fall adapter so that the sphere hits the floor switch when it is released.
2. Measure the height. Be thinking about the uncertainty of this measurement.
3. Click the Record icon () in the Experiment Setup WIndow.
4. Put the sphere back in the adapter, and "let fly".
5. Record the height of fall in the Keyboard Sampling window, and click <Enter>. Check the acceleration calculation in the data table. If it is unreasonable, find what is wrong, and fix it.
6. Repeat steps 4 and 5 several times for this height. Once the software gets the idea that you will be keeping the same height, you won't have to retype it - just press <Enter>.
7. When you have enough data (Ha!), click on "Stop Sampling". Change the height, and go back to step 1.
8. Continue until you have taken data for several heights over as wide a range as practical.

---

Results:

Have the Science Workshop^TM program calculate statistics () for the time of fall for each run. Open the Graphical Analysis^TM program, and transfer the mean time of fall and the height for each run to the Graphical Anslysis^TM data table. Add a column to the data table and place the formula for t² ("=t^2" or "=t*t") in it.

Construct a graph of t² vs. height. Add error bars to the graph. (You can get a pretty good idea of the uncertainty of the time of fall from examining the original data and the data statistics in the Science Workshop^TM data table.) Draw the best fit regression line, and get regression statistics for the line. You can calculate "g" fronm the slope of this line, right? Also, be sure to determine the uncertainty in your value of "g". What is the percent of difference between your calculated value and an "accepted value" of "g" (consult the Handbook of Physics & Chemistry)?

---

Conclusions:

So, what do you think? In particular,

• How does your value of "g" compare to an "accepted value"?
• Why is it that the slope of a t² vs. h graph yielded a value of "g"?
• What was the measurement that contributed the most uncertainty to your results? How could this be improved if you were to do this experiment again?

---

[Lab Index]