AP Physics - Experiment 2

Period of SHM

(low-tech version)

[Prev][Next][Up][Home][Help][Lab Index]

BHS -> Staff -> Mr. Stanbrough -> AP Physics-> AP Labs-> this page

Purpose:

I'm sure you've noticed that if you attach an object to the end of a hanging spring and release it, the object vibraates up and down. We will study this motion, called simple harmonic motion (SHM), later in some detail. For now, though, just notice that the period of the vibration (the time to repeat the motion once) depends on the mass of the attached object. A physicist would ask "How does the period of this motion depend on the mass?"

So, the purpose of this experiment is to answer the question, "How is the period of the simple harmonic motion (SHM) of an object attached to a spring related to the object's mass?"

The theoretical prediction for the relationship between period and mass in SHM (we will study this later) is that the period is proportional to the square root of the mass, so we could ask "Is the period of motion of a spring in SHM proportional to the square root of the mass of the attached object?"

Discussion:

The mathematical relationship between period and mass may not be quite as obvious as the relationship between force and stretch in the first experiment. However, you proceed in much the same way. You collect data - measuring the period of vibration over as wide a range of masses as possible - with an eye toward drawing mass vs. period graphs for particular springs. As you do so, you need to keep in mind the burning question "What is the precision of this measurement?".

There is an important experimental technique that you can use to increase the precision of the period measurement. Suppose that you can time an interval (using a stopwatch) to a precision of +/- 0.4 s . Then, suppose that you time one period of vibration of a mass and get a value of 2.0 s. This is 2.0 +/- 0.4 s, which has a measurement uncertainty of 25% - not very impressive.

Suppose, however, that we timed 20 periods of the motion, which took 40.0 s. The period is (40.0 s)/20 = 2.00 s (note the significant digits) and the uncertainty is (0.4 s)/20 = 0.02 s, so this measurement of period is 2.00 +/- 0.02 s which is a 1% measurement!

Equipment:

assorted small springs

ring stand

set of known masses

ring-stand clamp

c-clamp

stop watch

Safety Notes:

lab apparatusSetup:

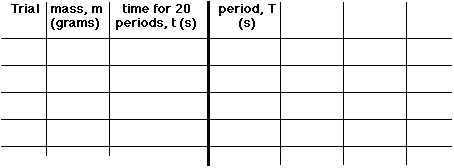
  1. Construct a data table. You need to record mass and period for each spring. Leave a few blank columns in your data table to use for calculations later. Part of a sample data table is shown below.

    sample data table
  2. Assemble the apparatus as shown in the photo. Be sure to clamp the ring stand to the lab table, or weight it with several books. Otherwise, the photo is just a suggestion - you might well come up with a better way. If your apparatus differs significantly from the suggested apparatus, you need to carefully describe it in your lab report, in case someone wants to try to replicate your results.

Procedure:

  1. For each trial, record the mass attached to the spring, and the time for 20 (or so) periods of the motion.
  2. You may assume that the masses are within 2% of the marked value. You can get a "feel" for the uncertainty in your timing measurement by repeating the measurement several times and comparing the results. (Remember to record all data.) Record your precision estimate in the data table.
  3. Repeat for at least one other (different) spring, using a separate data table for each spring.

Results:

  1. Calculate the period of vibration for each trial.
  2. Construct a graph of period vs. mass for each spring. Theory predicts that the best smooth curve through these data points will not be a straight line (but, of course, "you get what you got").
  3. Add another column to each data table for "square root of mass, m1/2". (Units will be grams1/2) Calculate this value for each trial.
  4. Construct a graph of period vs. mass1/2 for each spring. Is this graph (more or less) a straight line?

Conclusions:

Go back and re-read your statement of purpose for this lab. Now, answer the question. Here are some additional points you might want to cover:

  1. Are your graphs of period versus mass1/2 straight lines? What does this result mean?
  2. How confident can you be in your results? Why do you think so?
  3. What measurement contributed the most uncertainty to your results? What could be done to improve it?

[Prev][Next][Up][Home][Help][Lab Index]

BHS -> Staff -> Mr. Stanbrough -> AP Physics-> AP Labs-> this page

last update July 9, 2003 by JL Stanbrough