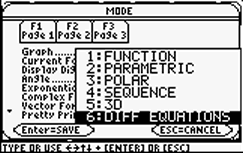
Press  and select "DIFF EQUATIONS" from the "Graph ..." menu. Press and select "DIFF EQUATIONS" from the "Graph ..." menu. Press  to save your choices. to save your choices. |
|
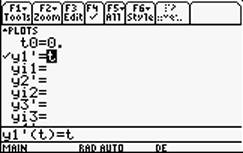
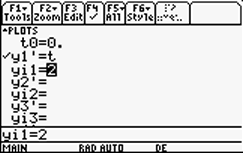
Press   to access the "y=" screen. Type your differential equation on the "y1' =" line. The independent variable must be "t". The screen shot at right shows the simple differential equation y'(t) = t entered as y1'. to access the "y=" screen. Type your differential equation on the "y1' =" line. The independent variable must be "t". The screen shot at right shows the simple differential equation y'(t) = t entered as y1'. |
|
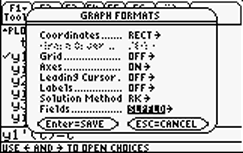
Press  to access the "Tools" menu. Select to access the "Tools" menu. Select  to access the Graph Formats Dialog. You can select either "Euler" or "RK" from the "Solution Method" menu, but be sure that you select "SLPFLD" from the "Fields..." menu. When everything is OK, press to access the Graph Formats Dialog. You can select either "Euler" or "RK" from the "Solution Method" menu, but be sure that you select "SLPFLD" from the "Fields..." menu. When everything is OK, press  to save your choices. to save your choices. |
|
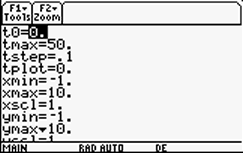
Pressing   accesses the almost-normal window screen. Notice that it contains the parameters t0 (starting t value), tmax (ending t value), and tstep (increment in t) in addition to the normal x and y window dimension parameters. If you find that a graph of your differential equation does not fill the screen, you can adjust the t0 and tmax values. Change tstep to increase/decrease the accuracy (and time taken) of the numerical solution. accesses the almost-normal window screen. Notice that it contains the parameters t0 (starting t value), tmax (ending t value), and tstep (increment in t) in addition to the normal x and y window dimension parameters. If you find that a graph of your differential equation does not fill the screen, you can adjust the t0 and tmax values. Change tstep to increase/decrease the accuracy (and time taken) of the numerical solution. |
|
Press   to graph the slope field. to graph the slope field. |
|
To graph a solution to the differential equation, you need to enter the initial conditions. There are (at least) two ways to do this. The most flexible way is to press   (F8). The calculator will prompt you to enter a value for "t" and a value for "y1". Starting at that point, the calculator will generate a numerical solution using either the Euler or the Runge-Kutta algorithm (which you selected from the Graph Formats Dialog ( (F8). The calculator will prompt you to enter a value for "t" and a value for "y1". Starting at that point, the calculator will generate a numerical solution using either the Euler or the Runge-Kutta algorithm (which you selected from the Graph Formats Dialog (  ) in step 2 above. You may press ) in step 2 above. You may press   as many times as you like to plot multiple solutions on the same screen. as many times as you like to plot multiple solutions on the same screen. |
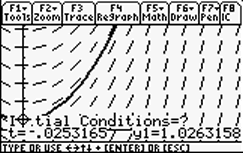 |
An alternate method for supplying initial conditions is on the "y=" screen (  ). If you enter a value for "yi1 =" (directly under the "y1' = " line), this value will be used as an initial value at t = 0. In other words, in the screen shot at right the initial conditions are t = 0, y = 2. You can enter multiple initial conditions using a list: {2, 4, 6} for example. ). If you enter a value for "yi1 =" (directly under the "y1' = " line), this value will be used as an initial value at t = 0. In other words, in the screen shot at right the initial conditions are t = 0, y = 2. You can enter multiple initial conditions using a list: {2, 4, 6} for example. |
|