

|
Consider Example 6 on page A30 in the Stewart text: "Find
all values of x in the interval The result of entering this function into the TI-89's
solve function as "solve(sin(x)=sin(2x),x)" is shown at
right. (You can get the solve function by pressing
The calculator has delivered several solutions ( the right-pointing arrow on the solution line indicates that there are more solutions on the line), but they are approximations. This may or may not be good enough. |
 |
|
In order to help the TI-89 find exact solutions, we can follow the lead of Example 6 and realize that sin 2x = 2 sin x cos x, which reduces all of the functions to the same argument. Entering "solve(sin(x)=2sin(x)cos(x),x)" produces the result shown at right. Well, the good news is that the TI-89 has produced exact
solutions for this version of the equation. The bad news is
that you probably have no idea what they are. Here's the
deal: In the expression
(Notice that only one of these solutions is in the domain
of the problem.) In this way, you can find all of the
solutions that fall in the interval |
 |
|
Is there an easier way? Yes, sometimes. The screen shot
at right shows what happens when you specify the domain of
solution to the solve command. Here, adding Note: You get the "greater than or equal" sign by
pressing |
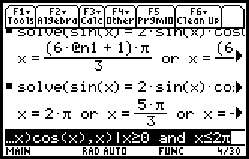 |