Inverse Secant - New

under construction

To investigate the graph of y = sec-1x, we need a graph of y = sec x. The easiest way to produce a graph of y = sec x is to start with a graph of y = cos x.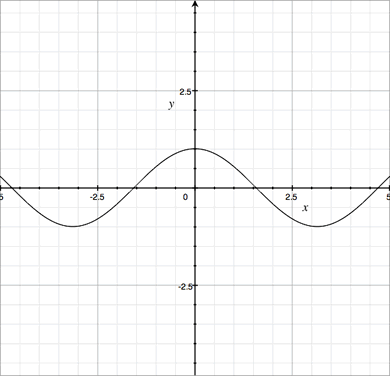

From the graph of y = cos x it is easy to produce the graph of y = sec x = 1/cos x. The graph of y = sec x has a vertical asymptote where cos x = 0.

 

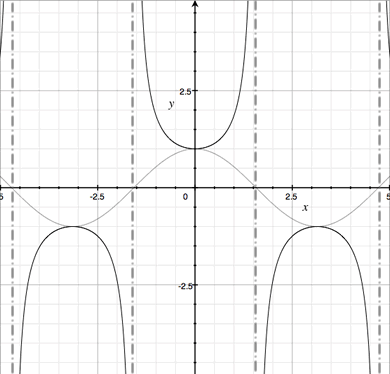Now, select the largest possible domain of y = sec x that is one-to-one. There is a slight difficulty here, since opinions differ as to which sections of the graph to pick. At right, the branches of the graph for the domain[0,pi/2) and [pi,3pi/2) have been chosen (highlighed in blue). The range is abs(y) >= 1.

For another opinion, click here.

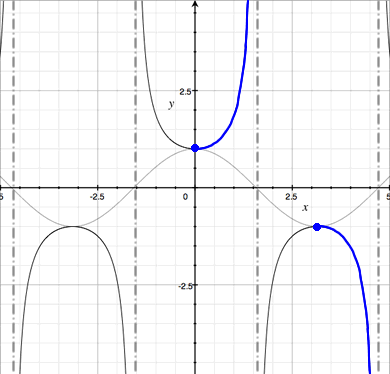You can obtain the graph of y = sec-1x (shown in red) by flipping the selected part of the graph of y = sec x (shown in blue) across the line y = x.

The domain of sec-1x is abs(x) >= 1 and the range is range.
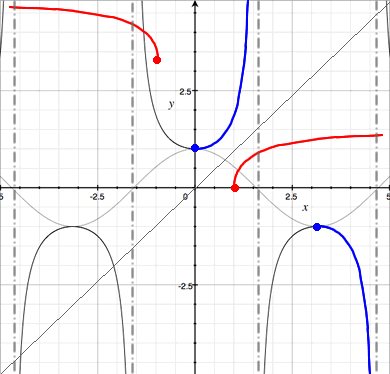Inverse secant and its derivative ...