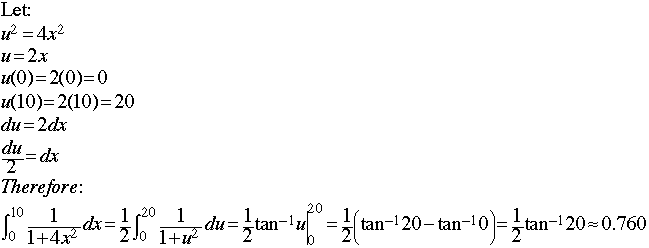Understanding the

Inverse Tangent Function

under construction

The Function y = tan -1x = arctan x and its Graph:

Since y = tan -1x is the inverse of the function y = tan x, the function y = tan -1x if and only if tan y = x. But, since y = tan x is not one-to-one, its domain must be restricted in order that y = tan -1x is a function.

To get the graph of y = tan -1x, start with a graph of y = tan x. (The window at right is [-2pi , 2pi] x [-4, 4]. )

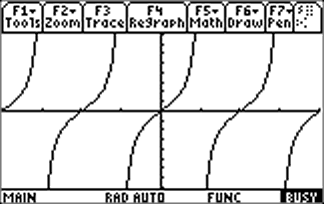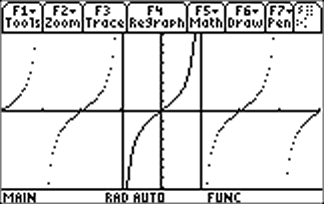Restrict the domain of the function to a one-to-one region - typically(-pi/2, pi/2) is used (highlighted at right) for tan -1x. This leaves the range of the restricted function unchanged as (-inf, inf).

Reflect this graph across the line y = x to get the graph of y = tan -1x (y = arctan x), the thickest black curve at right.

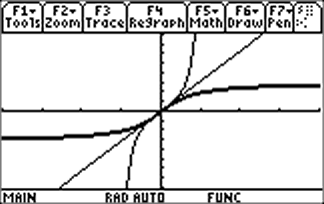Notice that y = tan -1x has domain (-inf, inf) and range (-pi/2, pi/2). It is strictly increasing on its entire domain.

So, when you ask your calculator to graph y = tan -1x, you get the graph shown at right. (The viewing window is [-2pi , 2pi] x [-4, 4].)

The Derivative of y = tan -1x:

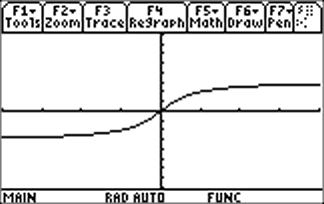The derivative of y = tan -1 x is: (Click here for a derivation.)

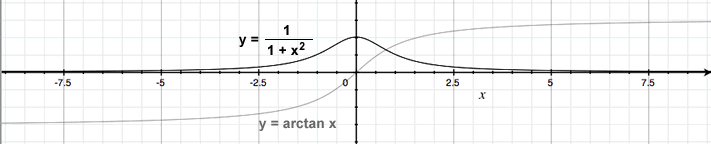
The graphs of y = tan -1 x and its derivative is shown below. The domain of y' is (-int, inf). Since y = tan -1 x is always increasing, y' > 0 for all x in its domain.

deriv of arctan x

Integrals Involving the Inverse Tangent Function

Here is a typical problem:

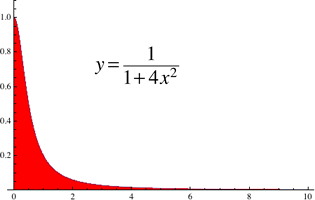graph of y = 1/(1+4x^2)What is the area under the graph of y = 1/(1+4x^2) on [0,10]?

The graph of this region is shown at right. The area of this region is:

area = int(1/(1+4x^2),x,0,10)

Now, we know that:

int(1/(1+u^2),u)=arctan u

Comparing what we know with what we need to know suggests that we let u2 = 4x2:

solution
last update March 30, 2010 by Jerry L. Stanbrough