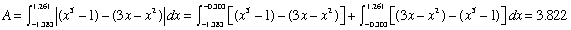6.1 Area Between Curves
Notes
- Calculating area of a region as the difference of two areas
- sketch the graphs of y = x2 + 3, y = x/2 + 1, x = 0, and x = 4. Lightly shade the area enclosed by these graphs.
 This is a [-0.5,5] x [-1,25] window.
This is a [-0.5,5] x [-1,25] window.
- Demonstrate the "Shade" operation on the TI-89 (F5 Menu - A) .
- A Riemann approximation
- Approximate the area between the graph of y = x2 + 3 and the x-axis on [0, 4] using a Riemann sum with n = 4 and left-hand endpoints. Be sure to draw the rectangles! Call this approximation Atop.
(Atop = 1(3 + 4 + 7 + 12) = 26
- Review the Riemann sum function on the TI-89.
- Approximate the area between the graph of y = x/2 + 1 and the x-axis on [0, 4] using a Riemann sum with n = 4 and left-hand endpoints. Be sure to draw the rectangles! Call this approximation Abottom.
Abottom = 1(1 + 3/2 + 3 + 5/2) = 7
- A = Atop - Abottom.
A = 26 - 7 = 19
- Using a definite integral
- Write a definite integral that expresses the area between the graph of y = x2 + 3 and the x-axis on [0, 4]. Emphasize how the definite integral expresses the sum of rectangles. Evaluate this integral. Call this area Atop.
Atop = 100/3 = 33.333
- Write a definite integral that expresses the area between the graph of y = x/2 + 1 and the x-axis on [0, 4] and left-hand endpoints. Emphasize how the definite integral expresses the sum of rectangles. Evaluate this integral. Call this approximation Abottom.
Abottom = 8
- A = Atop - Abottom
A=100/3 - 8 = 76/3 = 25.333
- Limitation: The definite integral only represents the area between the function and the x-axis where the function is non-negative.
- Calculating area of a region as a single area
- Regraph the functions in part A.
- A Riemann approximation
- Approximate the area between the graph of y = x2 + 3 and the graph of y = x/2 + 1 on [0, 4] using a Riemann sum with n = 4. Be sure to draw the rectangles!
A = 1(
2 + 5/2 + 5 + 19/2) = 19
- Using a definite integral
- Write a definite integral that expresses the area between the graph of y = x2 + 3 and the graph of y = x/2 + 1 on [0, 4]. Emphasize how the definite integral expresses the sum of rectangles. Evaluate this integral.
A = 76/3 = 25.333
- One function has some negative values
- Find the area enclosed by the graphs of y = x2 + 3, y = 1- x, x = 0, and x = 4.
- Sketch the graphs and locate the enclosed area.
- Draw some representative rectangles.
- Finding the height of the rectangles
- Finding the base of the rectangles
- Construct a definite integral
- Evaluate
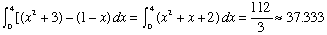
- Both functions have negative values
- Find the area enclosed by the graphs of y = -1 - x2, y = -x - 4, x = -1, and x = 1.
- Sketch the graphs and locate the enclosed area.
 Window is [-2, 2] x [-6, 1]
Window is [-2, 2] x [-6, 1]
- Construct the definite integral and evaluate.
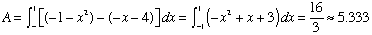
- Finding points of intersection
- Find the area enclosed by the graphs of y = x2 and y = x.
- Sketch the graphs and locate the enclosed area.
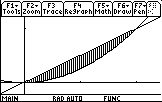 Window is [-.2, 1.2] x [-.2, 1.2]
Window is [-.2, 1.2] x [-.2, 1.2]
- Where do the graphs intersect? Solve x2 = x for x. Factor x2 - x = 0.
- Construct the definite integral and evaluate.
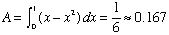
- Find the area enclosed by the graphs of y = -1 - x2, y = -x - 4.
- Sketch the graphs and locate the enclosed area.
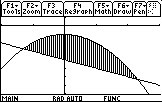 Window is [-2, 3] x [-8,1]
Window is [-2, 3] x [-8,1]
- Where do the graphs intersect? -1 - x2 = -x - 4
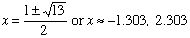
- Construct the definite integral and evaluate.
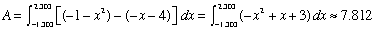
- Multi-part Areas
- Find the area enclosed by the graphs of y = sin x and y = x/2 between x = 0 and x =
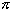 .
.
- Sketch the graphs and locate the enclosed areas.
 Window is [0, 3.5] x [-0.2, 2.2]
Window is [0, 3.5] x [-0.2, 2.2]
- Where do the graphs intersect? sin x = x
x = 1.895
- Construct the definite integrals and evaluate.
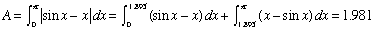
- Areas bounded by relations
- Find the area enclosed by the graphs of x = y2 - 4y and x = 2y - y2. (This is problem #4, p. 308 in Stewart)
- Method 1 - the direct approach
- Sketch the graphs and locate the enclosed area. Here, your calculator won't help! Plot some points and use your knowledge of the graphs of parabolas.
- Where do the graphs intersect? Where y2 - 4y = 2y - y2.
y = 0 or y = 3, so the points of intersection are (0, 0) and (-3, 3)
- Construct the definite integral and evaluate.
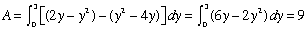
- Method 2 - using the inverse
- Find the inverse of each relation by switching all y's to x's and switching all x's to y's.
y = x2 - 4x and y = 2x - x2.
- Proceed as before
 Window is [-1, 4] x [-8, 5]
Window is [-1, 4] x [-8, 5]
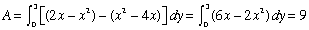
- Find the area enclosed by the graphs of y = (x + 1)1/5 and x = 3y - y2.
- Even though only one equation is a relation, you can still find the inverse of each.
x = (y + 1)1/5 , so y = x5 - 1, and y = 3x - x 2.
- Proceed as before:
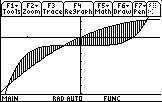 Window is [-1.5, 1.5] x [-7, 2.5]
Window is [-1.5, 1.5] x [-7, 2.5]
x5 - 1 = 3x - x 2 gives x = -1.383, -0.303, 1.261
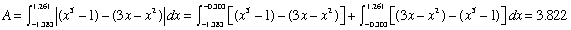
last update January 1, 2007 by JL Stanbrough
 This is a [-0.5,5] x [-1,25] window.
This is a [-0.5,5] x [-1,25] window.
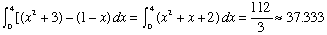
 Window is [-2, 2] x [-6, 1]
Window is [-2, 2] x [-6, 1]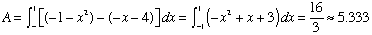
 Window is [-.2, 1.2] x [-.2, 1.2]
Window is [-.2, 1.2] x [-.2, 1.2]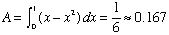
 Window is [-2, 3] x [-8,1]
Window is [-2, 3] x [-8,1]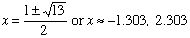
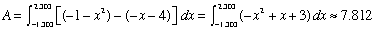
 .
.
 Window is [0, 3.5] x [-0.2, 2.2]
Window is [0, 3.5] x [-0.2, 2.2]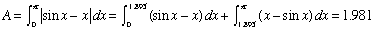
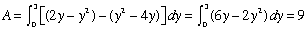
 Window is [-1, 4] x [-8, 5]
Window is [-1, 4] x [-8, 5]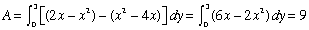
 Window is [-1.5, 1.5] x [-7, 2.5]
Window is [-1.5, 1.5] x [-7, 2.5]