| Terms | |
|---|---|
Sequence |
a list of numbers, usually separated by commas (t1, t2, t3, ...) (Technically, a sequence is a function whose domain is the natural numbers.) |
Term |
one of the numbers in a sequence or series |
Arithmetic Sequence |
a sequence in which the difference between successive terms is constant |
Common Difference |
the difference between successive terms in an arithmetic sequence |
Geometric Sequence |
a sequence in which the ratio of successive terms is constant |
Common Ratio |
the ratio of successive terms in a geometric sequence |
Finite Sequence |
a sequence that has a last term |
Infinite Sequence |
a sequence that does not have a last term |
Series |
the sum of a sequence (t1 + t2 + t3 + ...) |
Arithmetic Series |
a series based on an arithmetic sequence (the sum of the terms of an arithmetic sequence) |
Geometric Series |
a series based on a geometric sequence (the sum of the terms of a geometric sequence) |
Finite Series |
a series based on a finite sequence (the sum of the terms of a finite sequence) |
Infinite Series |
a series based on an infinite sequence (the sum of the terms of an infinite sequence) |
Partial Sum |
the sum of a finite number of terms of a series |
Sequence of Partial Sums |
every infinite series has a sequence of partial sums = first term, sum of first two terms, sum of first three terms, sum of first four terms, etc. |
Converges |
If the sum of an infinite series has a limit, the series converges. |
Diverges |
If the sum of an infinite series has no limit, the series diverges. |
Explicit Definition |
tells how to calculate any specified term in a sequence or series |
Implicit Definition |
tells how to construct a sequence or series by building it term-by-term starting with the first term |
Limit |
a number that the terms of a sequence (or partial sums of a series) gets closer to as the number of terms increases |
n approaches infinity |
the number n gets larger and larger (forever) |
| limit of some expression equals infinity | the value of the expression gets larger and larger (forever) |
| Symbols | |
|---|---|
| n | the number of the current (or next) term in a sequence or series |
| t | the value of a term in a sequence or series |
| d | the common difference of an arithmetic sequence or series |
| r | the common ratio of an geometic sequence or series |
| tn | the value of the current (or next) term in a sequence or series |
| tn-1 | the value of the previous term in a sequence or series (the term before the nth term) |
| S | the value of a series (the sum of terms) |
| Sn | the (partial) sum of the first n terms of a series |
| Sn-1 | the (partial) sum of the first n - 1 terms of a series (the sum of all the terms before term number n) |
| What happens to the value of the expression as the number of terms in its sequence (or series) gets larger and larger? | |
| Recursive Definitions | |
|---|---|
| Step 1 | Where does the sequence or series start? What is the first term (t1)? |
| Step 2 | How do you calculate the next term (tn ) of the sequence or series based on the terms you have so far? The last term so far is tn-1. The second to the last term so far is tn-2, etc. |
| Formulas | |
|---|---|
| Explicit Definition of an Arithmetic Sequence | tn = t1 + (n - 1)d |
| Explicit Definition of a Geometric Sequence | tn = t1rn-1 |
| Sum of a Finite Arithmetic Series | |
| Sum of a Finite Geometric Series | |
| Limit of a Rational Function | 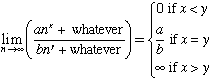 |
| Limit of a Power Function | |
| Sum of an Infinite Geometric Series | 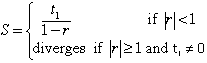 |
last update December 18, 2007 by JL Stanbrough