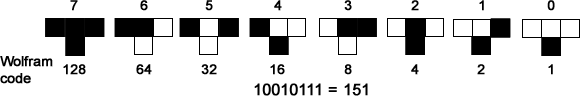
When we write a number, like 5326, we all believe that we know what we are talking about - but what, exactly, are we talking about? We don't mean 5 + 3 + 2 + 6 or 5 x 3 x 2 x 6. What we mean is (5 x 1000) + (3 x 100) + (2 x 10) + (6 x 1). Our system of numerals is a place-value system. The 6 is in the one's place, the 2 is in the 10's place, and so on. Notice that (5 x 1000) + (3 x 100) + (2 x 10) + (6 x 1) = (5 x 103) + (3 x 102) + (2 x 101) + (6 x 100). We understand that the numeral in each place needs to be multiplied by 10place number, where the place numbers start at zero.
It has been widely conjectured that our place-value system is based on tens because people (usually) have ten fingers (and ten toes). What then, would our ancestors have done if they had sixteen fingers and sixteen toes? In that case, the number 5326 would likely mean (5 x 163) + (3 x 162) + (2 x 161) + (6 x 160). This is called a "base-16" number. There is nothing "sacred" about using 10 as a base for numerals - base 16 works the same way. In fact, base-16, or hexadecimal, numbers are often used in computer science, because they fit the situation more-naturally that base-10 numbers.
Our common base-10 number system uses ten digits, 0-9, because each of the "places" could have one of ten different values. In other bases, you have different numbers of digits - base-16 requires 16 digits (They are 0-9, A = 10, B = 11, C = 12, D = 13, E = 14,F = 15.) base-5 requires only 5 digits (0-4), base-2 uses only 2 digits (0 and 1).
It turns out that base-2 numbers are also particularly useful in computer science, because, for instance, a memory location (bit) can be either "on" (1) or "off" (0). So a useful shorthand for "on, off, off, on, off, on, on, on" is the binary number "10010111".
The base-2 number "10010111" means (1 x 27) + (0 x 26) + (0 x 25) + (1 x 24) + (0 x 23) + (1 x 22) + (1 x 21) + (1 x 20) = (1 x 128) + (0 x 64) + (0 x 32) + (1 x 16) + (0 x 8) + (1 x 4) + (1 x 2) + (1 x 1) = 151 (in base-10).
Binary numbers are very convenient for describing the rules for elementary cellular automata.Why bother? Let's examine a typical rule. First, in English:
(0)"If the current cell is 'off' and both of its neighbors are 'off', it becomes 'on' in the next generation, (2) but if the current cell and its neigbor to its (our) left is 'off' but the neighbor to its (our) right is 'on', the cell becomes 'on' in the next generation, (4) but if the current cell is 'on' but both neighbors are 'off', it stays on in the next generation,(8) but if the current cell and it's right neighbor are both 'on', but the left neighbor is 'off', it turns 'off', (16) but if the current cell and its right neighbor are both 'off'' and its left neighbor is 'on', it turns 'on', (32) but if the current cell is 'off' and both neighbors are 'on', it turns 'off', (64) but if the cell and its left neighbor are both 'on' and the right neighbor is 'off', it turns 'off', (128) but if the current cell and both its neighbors are 'on', it stays 'on'."
By any measure, this is not a good way to describe a rule. You gave up reading it before you were halfway through, didn't you?. Luckily, rules for elementary cellular automata can also be described graphically, as follows:
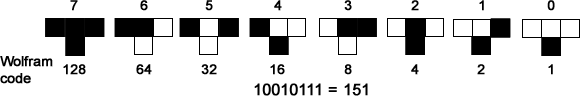
This is the same rule described in English above. The graphical form is very convenient when you are trying to construct the output of a rule, but it is not very handy for describing the CA, because it's not easy to tell two rules apart if they only differ by one or two "on"s and "off"s. However,, a rule can be summarized as an 8-bit (place) base-2 number, like this:
"10010111" = 151
It is very easy to talk about rules using this notation. You can just say "Rule 151". This is why CAs are often referred to by their code numbers.
You have seen some examples of converting base-2 numbers into base-10 numbers, but what is someone gives you a base-10 rule number - how do you tell where the "on"s and "off"s go?
Suppose someone mentions the Rule 150 CA. What does that look like graphically? The conversion is easily done by repeated subtraction. The process is demonstrated in the table below.
Converting the Base-10 Number 150 to Base-2 |
|
Step |
Result |
| Start at the left-most place - the 128's place. If you can subtract 128 from the number (and get a non-negative result), do so (150 - 128 = 22) and put a "1" in this place. Otherwise, put a "0". | 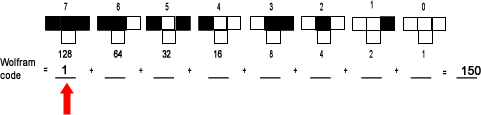 |
| Can you subtract 64 from 22? No. The 64's place digit is "0". | 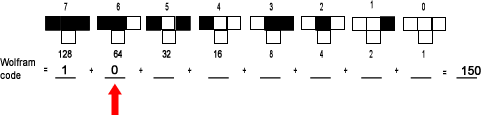 |
| Can you subtract 32 from 22? No. The 32's place digit is "0". | 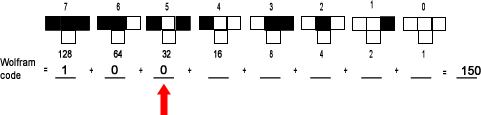 |
| Can you subtract 16 from 22? Yes, 22 - 16 = 6. The 16's place digit is "1". | 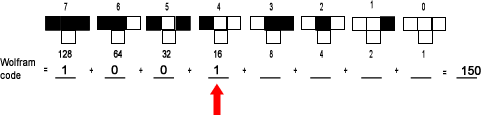 |
| Can you subtract 8 from 6? No. The 8's digit is "0". | 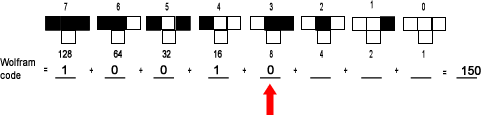 |
| Can you subtract 4 from 6? Yes, 6 - 4 = 2. The 4's place digit is "1". | 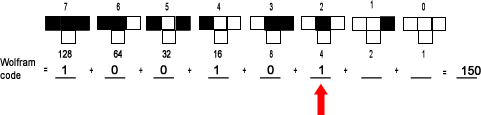 |
| Can you subtract 2 from 2? Yes, 2 - 2 = 0. The 2's place digit is "1". | 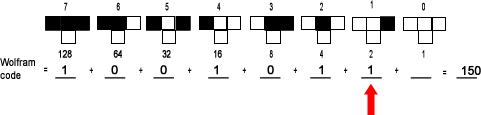 |
| Can you subtract 1 from 0? No. The 1's digit is "0". Actually, once you get a result of 0 you can fill in all of the remaining places with 0's. |
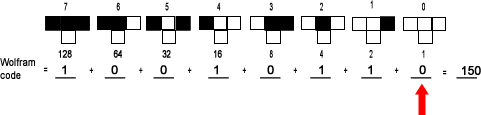 |
| 1's represent a black cell in the next generation, while 0's represent a white cell. Just fill in the rule and you are done! |  |
Therefore, rule 150 in binary form is "10010110".
Of course other number bases are possible, but are they useful? Well, yes. For instance, we will be branching out into CAs that can have three states per cell - it is easiest to specify their codes using base-3 numbers. For instance, the rule "10220012" = (1 x 37) + (0 x 36) + (2 x 35) + (2 x 34) + (0 x 33) + (0 x 32) + (1 x 31) + (2 x 30) = (1 x 2187) + (0 x 729) + (2 x 243) + (2 x 81) + (0 x 27) + (0 x 9) + (1 x 3) + (2 x 1) = 2840 (in base-10). There are a lot more possible rules using 3-state cells!
last update November 23, 2009 by JL Stanbrough