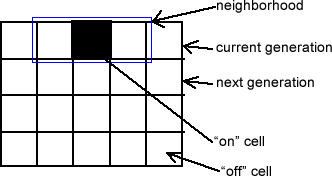
 Each square in the grid is called a cell.
Each square in the grid is called a cell.
In a one-dimensional CA, each horizontal row of cells represents a generation. The top row is the starting generation.
The starting pattern of cells is called the seed or initial state of the CA. The most common seed for an elementary CA is a single "On" cell surrounded by "Off" cells on the top row of the grid, but other configurations are certainly possible (and often interesting).
The state of a cell describes its current condition - alive, dead, growing, shrinking, moving, etc. In an elementary CA, each cell can have only one of two states - "On"/"Off", "Alive"/"Dead", or graphically, "Black"/"White".
The neighborhood of a cell consists of all of the cells that can influence its behavior in the next generation. The neighborhood of an elementary CA consists of the cell itself and the two cells immediately to its left and right. (This is called an r = 1 CA.) A complication arises - who are the neighbors of the border cells? One solution is to imagine the current generation to extend infinitely far to the left and right, so that the grid we see is just a small slice of the "universe." That is what we will generally do. However, another common solution is to imagine that the right edge of the grid folds around and connects to the left edge of the grid, forming a tube-shaped universe. Therefore the left neighbor of the leftmost cell is the rightmost cell, and vice versa. It might seem reasonable to just imagine that the universe ends at the border of the grid, but that would mean that you would need special rules for the edge cells, and we want to keep things as simple as possible.
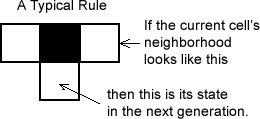 The rule for a CA tells the state of the current cell in the next generation based on the current state of its neighborhood.
The rule for a CA tells the state of the current cell in the next generation based on the current state of its neighborhood.
last update November 21, 2009 by JL Stanbrough