Let's Build a CA

There's just no way to get the feel for what is going on other than to actually try it. Here's a rule (What's its Wolfram code, by the way?):

To construct a CA using this rule, follow along with the step-by-step procedure shown below.

The First & Second Generation
Action	Result
Start at the top of a sheet of graph paper with one on/black cell. The top row represents the initial generation.
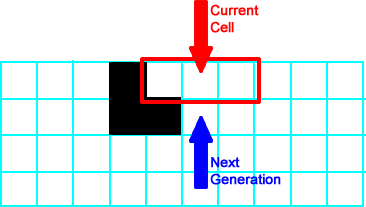
In the diagram at right, the current neighborhood is outlined in red, and the red arrow points to the current cell. All of the neighborhoods to the left of this one have the same neighborhood (neighborhood 0 = 3 empty cells) and follow which says that the current cell stays empty in the next generation. Therefore, all cells in the next generation from the current neighborhood to the left edge of the grid stay white/empty/dead/off.
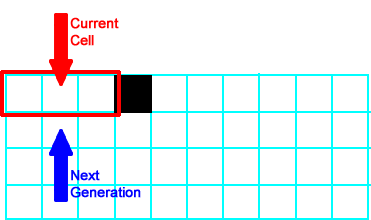Moving the current cell one cell to the right, the new neighborhood (neighborhood 1) follows 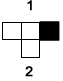so the current cell stays empty in the next generation.
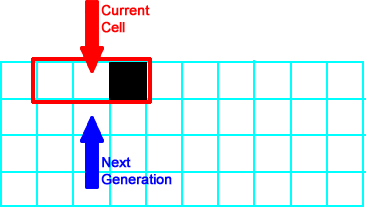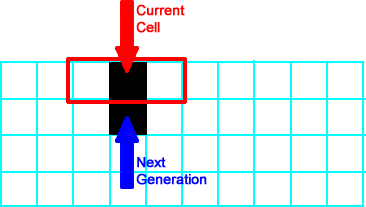
Now, the current cell is the black cell, and the neighborhood is 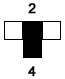(neighborhood 2) so the current cell stays black in the next generation.
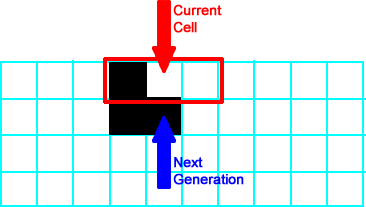
This neighborhood is 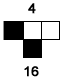so the current cell turns on for the next generation.
All the rest of the neighborhoods in this generation look like 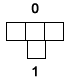so no other cells change in this generation. This completes the second generation. It consists of the two black cells shown.

The Third Generation:

Building the Third Generation
Action	Result
All of the cells to the left of the current neighborhood areand so the next generation stays empty for those cells.
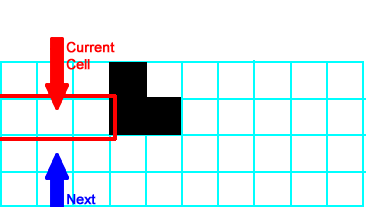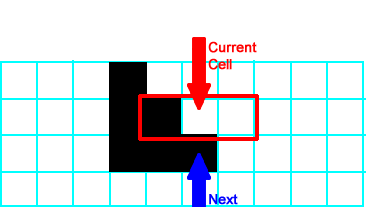
Moving one cell to the right, the new neighborhood (neighborhood 1) follows 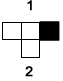so the current cell stays empty in the next generation.
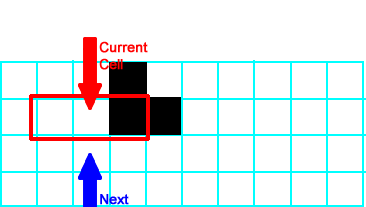The neighborhood is 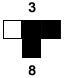. The current cell stays on.


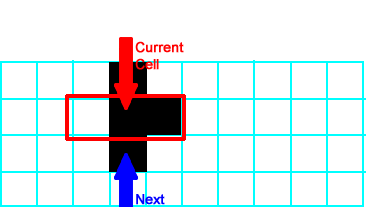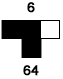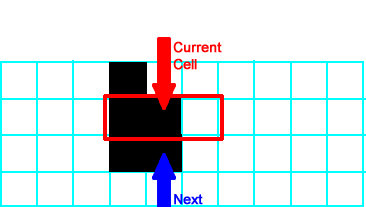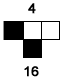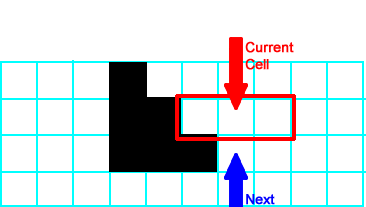
All the rest of the neighborhoods look like so no other cells change in this generation. This completes the second generation, which consists of a row of three black cells.

Let's Build a Cellular Automaton!