Let's modify the last rule slightly - simply change the neighborhood-0 output from white to black. The new rule is shown below:

What is the Wolfram code for this rule? With such a slight change in the rule, we ought to expect a sligh change in the output, right? Let's see.
The First Generation:
| Action | Result |
|---|---|
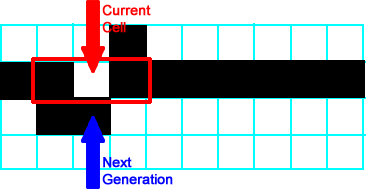
All of the neighborhoods to the left of the black cell are  , so all cells from the arrow leftward are black/on in the first generation. , so all cells from the arrow leftward are black/on in the first generation. |
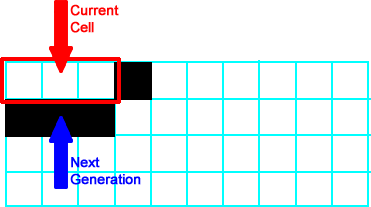 |
 |
 |
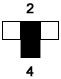 |
 |
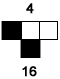 |
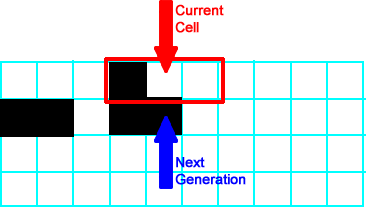 |
All neighborhoods from this one are  , so all remaining cells in this generation are black/on. This completes the first generation. , so all remaining cells in this generation are black/on. This completes the first generation. |
 |
| Action | Result |
|---|---|
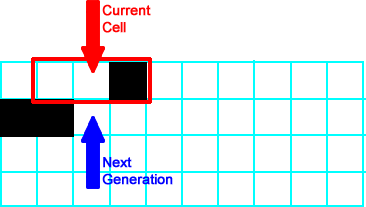
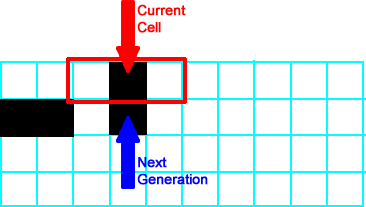
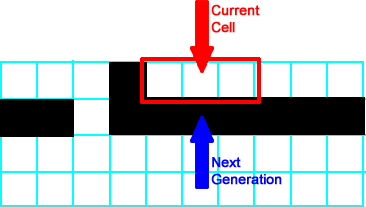
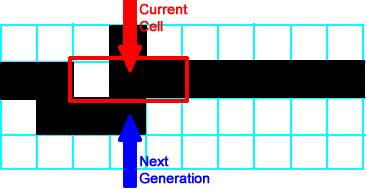
All neighborhoods to the left of the neighborhood shown follow 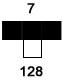 , so all of those cells produce a white/empty cell. The neighborhood shown at right is , so all of those cells produce a white/empty cell. The neighborhood shown at right is 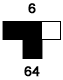 , so its successor is black/on. , so its successor is black/on. |
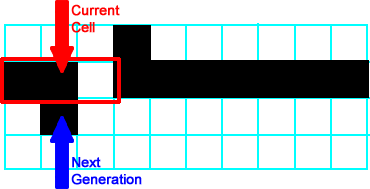 |
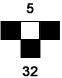 |
 |
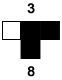 |
 |
All of the remaining cells are 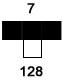 . This completes the second generation. . This completes the second generation. |
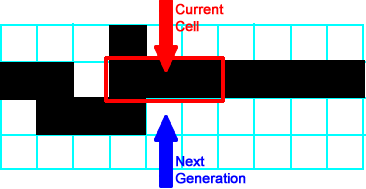 |
The third generation is  .
.
After eleven generations you should have  .
.
Switching to Mathematica (computer), the first 50 generations is: 
Making a tiny change in the rule certainly did not make a slight change in the output! This is a completely different pattern!
At this point, you should be able to answer the following questions. Check your answers here.
last update November 24, 2009 by JL Stanbrough