Totalistic Cellular Automata

What causes elementary cellular automata to have such interesting properties? Is it really that very simple instructions/rules can produce very complicated behavior, or is there just something about the way that we have implemented ECA's in our grids that causes this effect? Is the complicated behavior caused by the fact that we:

• use a square grid?
• use just 2 colors/states?
• determine the next generation by just looking at the two immediate neighbors of the current cell?
• update all cells in a generation simultaneously?
• allow all cells to "reproduce?"

(This is not a complete list!) In order to test the hypothesis (Simple rules can produce complicated behavior.) we would need to exhaustively check each of the possible objections one at a time by constructing and testing a new automaton. For instance, to check whether the effects we have seen are produced by a square grid, we would have to construct automata that did not have square grids (perhaps triangular or hexagonal grids) and show that their behavior is essentially the same as the behavior of the elementary cellular automata.

Such programs have been carried out, but we are not going to take the time to replicate them. Instead, we will examine a new type of automaton that has three colors instead of two, called a Totalistic Cellular Automaton.

Totalistic Neighborhoods and Rules:

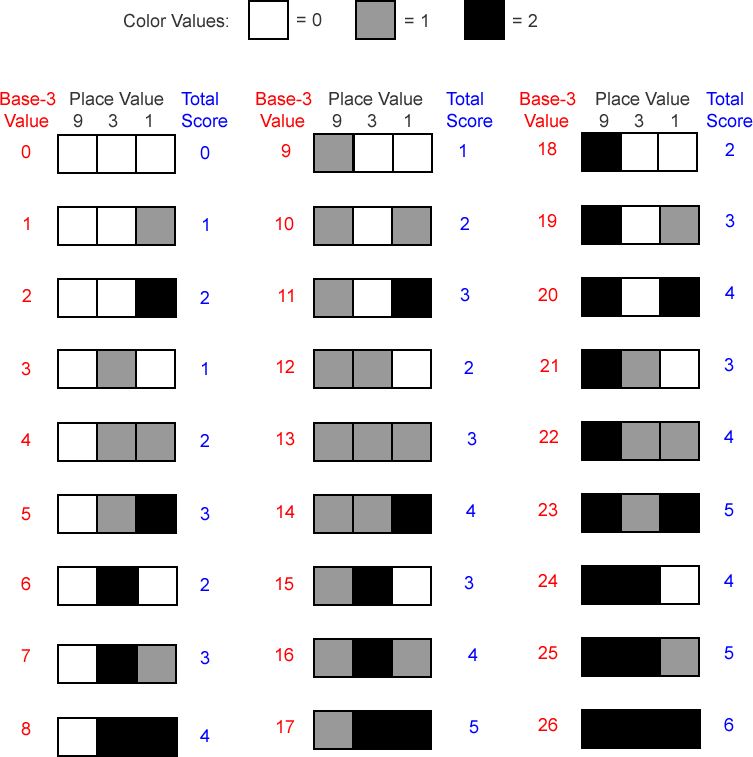
This automaton is called "totalistic" because it gives each color a numeric value and uses the total value of the colors of the current cell and its immediate neighbors to determine the state of the current cell in the next generation. If each cell can have any one of three colors, there must be (3)(3)(3) = 27 neighborhoods for a 3-color, r = 1, totalistic cellular automaton, shown below.

Using 3 colors, there are 33 = 27 different neighborhoods. Fortunately, using a totalistic rule we won't need 27 rules! As you can see at right, there are only 7 possible totals, 0-6, so only 7 rules are necessary. Since each of the 7 rules can have any of 3 possible states (0, 1, or 2), there are 37 = 2187 different 3-color, r = 1, totalistic cellular automata.