Kinematics Activity
Target Practice
![[Index]](../../../NavIcons/Up.GIF)
![[Home]](../../../NavIcons/Home.GIF)
![[Help]](../../../NavIcons/Help.GIF)
Purpose:
To predict the landing spot of a horizontally-projected
projectile. 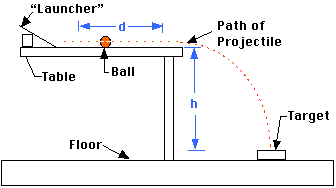
Discussion:
If you know the height of a table, you can calculate the time
required for a ball to fall from the table to the floor. If you know
the velocity of the ball as it leaves the table, you can calculate
the distance from the table at which the ball will hit the floor. You
can find the velocity of the ball if you know the time it takes to
roll a measured distance on the table.
In this lab, you will place a tin-can target at the predicted
landing spot of the ball. If the ball lands in the can the
first time, you get credit for the lab.
Notes:
- Accurate measurement and precise calculation are very
important in hitting the target. Be sure to use 9.80
m/s2 (= 980 cm/s2) for "g".
- Credit is given in this lab for hitting the target the
first time the ball hits the floor. Be sure that you catch
the ball before it leaves the table. If the ball hits the
floor at any time before your "official launch", you must change
your launcher to produce a significantly-different velocity
for the ball, and start over.
- If the ball misses the target to the right or left, it will
still count as a hit.
Equipment:
|
small sphere
|
meter stick
|
stop watch
|
string
|
|
tin can
|
tape
|
small weight
|
plastic ruler or book
|
|
calculator
|
worksheet
(ClarisWorks)
|
|
|
A calculation worksheet
(ClarisWorks) is available to help you organize your
calculations.
Procedure:
- Devise a "launcher" for the ball from a ruler or book -
anything with a smooth groove in it that the ball can roll down.
Find a starting point on the launcher that gives the ball a
reasonable velocity.
- Place 2 pieces of tape 30-50 cm apart on the lab table in the
path of the ball. This is distance "d" in the diagram above.
Record this distance. The distance that you use needs to be a
compromise:
- If the distance is too short, you will not be able to get
an accurate time for the ball to cover the distance, and your
velocity will not be accurate.
- If the distance is too long, friction will slow the ball
appreciably by the time it reaches the edge of the table, and
your calculated speed will not be the actual speed that the
ball has when it leaves the table.
- Measure the time (troll) it takes the ball to cover
this distance. It would be a good idea to time several trials and
calculate the average time. Record your data in a data table.
- Calculate the speed, vx, of the ball as it rolls
across the table. Show your calculation.
- Carefully measure the vertical distance from the top of the
lab table to the top of your target. This is "h" in the diagram
above. Record this distance.
- Calculate the time (the falling time, tfall) it
will take the ball to fall from the table top to the target. Show
your calculation.
- Calculate the horizontal distance that the ball will go during
the time it takes to fall to the target. Show your
calculation.
- Locate the point on the floor directly below the edge of the
table top where the ball leaves the table. You can do this
accurately by making a "plumb line" from a small weight and a
string.
- Measure the horizontal distance that the ball will go on the
floor, and place the target at that point.
- Call your instructor. While you wait:
- Are your measurements consistent and reasonable?
- Did you check your calculations?
- Is the target distance reasonable?
![[Index]](../../../NavIcons/Up.GIF)
![[Home]](../../../NavIcons/Home.GIF)
![[Help]](../../../NavIcons/Help.GIF)
last update September 18, 2007 by JL
Stanbrough