Projectile Lab
Projectiles - Horizontal Launch
![[Index]](../../../NavIcons/Up.GIF)
![[Home]](../../../NavIcons/Home.GIF)
![[Help]](../../../NavIcons/Help.GIF)
Purpose:
To determine if the kinematics of a projectile can really predict
the motion of a horizontally-launched projectile.
Discussion:
In this lab, you will check to see if the kinematics concepts and
equations we have discussed really predict the motion of an actual
projectile.
In this lab, you will measure the starting velocity of a
projectile and the distance from the table (the range, R) that the
projectile lands. From this, you can calculate the vertical distance
that it fell and compare your calculated value and the measured
value..
It is easy to record the location where the projectile lands on
the floor by placing a piece of carbon paper over a piece of scrap
paper taped to the floor. The projectile will leave a mark on the
paper where it hits. You can measure the horizontal range of the
projectile and compare this to the calculated distance.
Equipment:
|
small sphere
|
meter stick
|
stop watch
|
string
|
|
plastic ruler or book
|
tape
|
small weight
|
calculator
|
|
carbon paper
|
|
|
|
Procedure:
- Devise a "launcher" for the ball from a ruler or book -
anything with a smooth groove in it that the ball can roll down.
Find a starting point on the launcher that gives the ball a
reasonable velocity.
- Place 2 pieces of tape 30-50 cm apart on the lab table in the
path of the ball. This is distance "d" in the diagram above.
Record this distance. The distance that you use needs to be a
compromise:
- If the distance is too short, you will not be able to get
an accurate time for the ball to cover the distance, and your
velocity will not be accurate.
- If the distance is too long, friction will slow the ball
appreciably by the time it reaches the edge of the table, and
your calculated speed will not be the actual speed that the
ball has when it leaves the table.
- Carefully measure the vertical distance from the top of the
lab table to the floor. This is "h" in the diagram above. Record
this distance.
- From a trial run, find the approximate position where the
projectile hits the floor. Tape a piece of scrap paper at this
location, and put a piece of carbon paper face down over it to
mark the landing spot of the projectile.
- Launch the projectile several times.
- For each launch, measure the time it takes the
ball to roll the measured horizontal distance on the table, and
record the rolling times (troll) in a data
table.
- You should get a group of reasonably-close-together spots
on the "target" paper. If the spots are wildly far apart, you
need to adjust your launcher or launching technique to get more
consistency.
- Locate the point on the floor directly below the edge of the
table top where the ball leaves the table. You can do this
accurately by making a "plumb line" from a small weight and a
string. Measure the distance from this point to the center
(average) of your landing positions. This is the range of the
projectile ("R" in the diagram above).
- Change your launcher so that your projectile is launched at a
different speed and repeat. Take at least one set of data for each
person in your lab group.
Results: (Show a sample calculation!)
- Calculate the average rolling time (troll) for your
projectile to travel the measured horizontal distance (d).
- Calculate the speed, vx, of the projectile as it
rolls across the table (vx = d/troll). This
should be the speed that the projectile has when it leaves the
table.
- Calculate the time (the falling time, tfall) it
took the projectile to move the horizontal distance (range) R.
(Since R = vxtfall, tfall =
R/vx)
- Calculate the distance the ball will fall vertically from the
table top to the target. (
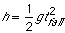 )
Note: Use g = 9.8 m/s2 for accuracy.
)
Note: Use g = 9.8 m/s2 for accuracy.
- A good measure of comparison (between the measured and
calculated heights) is the "percent of difference":
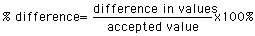
Conclusions:
How do the measured height and calculated height compare? In other
words, do the kinematics equations that we have been using seem to
work in practice? If not, why not? Do you think that it is the fault
of the kinematics or due to some problem with your experimental
procedure? Be specific.
![[Index]](../../../NavIcons/Up.GIF)
![[Home]](../../../NavIcons/Home.GIF)
![[Help]](../../../NavIcons/Help.GIF)
last update October 30, 2001 by JL
Stanbrough

