Conceptual:
 |
 |
|
|
|
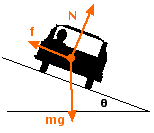
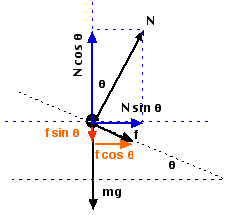 A
free-body diagram for the car is shown at left. Both the normal
force, N (blue components) and the friction force, f (red components)
have been resolved into horizontal and vertical components. Notice
that there are now 3 vectors in the vertical direction (there were 2
vectors in the no-friction
case), and:
A
free-body diagram for the car is shown at left. Both the normal
force, N (blue components) and the friction force, f (red components)
have been resolved into horizontal and vertical components. Notice
that there are now 3 vectors in the vertical direction (there were 2
vectors in the no-friction
case), and:
Using the approximation ![]() ,
where
,
where ![]() is the coefficient of friction, gives:
is the coefficient of friction, gives:
If the coefficient of friction is zero, this reduces to the same normal force as we derived for no-friction, which is reassuring. If the coefficient of friction is not zero, notice that the normal force will be larger than it was in the no-friction case. Now, in the horizontal direction:
Here, the term ![]() is friction's contribution to the centripetal force. Also, notice
again that if mu = 0, this result reduces to the same Fnet as the
no-friction case. Now, since the net force provides the centripetal
force to turn the car:
is friction's contribution to the centripetal force. Also, notice
again that if mu = 0, this result reduces to the same Fnet as the
no-friction case. Now, since the net force provides the centripetal
force to turn the car:
So, what can be done with this?
Suppose you want to negotiate a curve with a radius of 50 meters and a bank angle of 15o (See the Example 1). If the coefficient of friction between your tires and the pavement is 0.50, what is the maximum speed that you can safely use?
Continuing the derivation above, we can get:
First, note that if the coefficient of friction were zero, the expression given above for v would reduce to the same expression we derived for the no-friction case. This is always a good, quick check. Next, notice that this velocity is about twice the no-friction velocity from Example 1.
In Example 3, I noted that NASCAR race cars actually go through the turns at Talladega Motor Speedway at about 200 mi/hr. If that is the case, what coefficient of friction exists between the car's tires and the pavement?
First,
(It is not always "good form" to generate intermediate results in a calculation, of course, but we have a pretty "hairy" calculation coming up, so I think I can forgive myself for getting the units straightened out at this point. Notice that I've kept an extra significant digit in the result, though, just for safety's sake.) Now, if we continue working from the last equation above Example 4, we can cross-multiply and solve for mu:
Is this correct? Well, it is a reasonable answer, and notice that the units work out correctly, which is always a good, quick check.
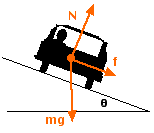
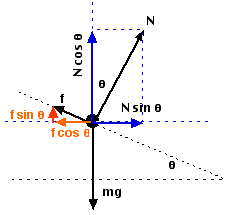 A
free-body diagram for the car is shown at left. Both the normal
force, N (blue components) and the friction force, f (red components)
have been resolved into horizontal and vertical components. Notice
that the friction force acts up the incline, to keep the car from
sliding toward the center of the turn. This derivation is very
similar to the previous case, and is left as an "exercise for the
reader".
A
free-body diagram for the car is shown at left. Both the normal
force, N (blue components) and the friction force, f (red components)
have been resolved into horizontal and vertical components. Notice
that the friction force acts up the incline, to keep the car from
sliding toward the center of the turn. This derivation is very
similar to the previous case, and is left as an "exercise for the
reader".