In section 9.6 of the text, Professor Hewitt discusses simulating gravity in outer space. Everything he says is correct, though it seems to lead to confusion on the part of many inquisitive and thoughtful students (Non-inquisitive, non-thoughtful students don't have questions, do they?). Most questions are either:
Here is another way of looking at the situation.
A long time ago, when we were discussing the differences between velocity and acceleration, I made the claim that you can't feel velocities, but you can feel accelerations. If you are a passenger in a car, you can tell when it speeds up, slows down, or turns a corner even with your eyes closed.
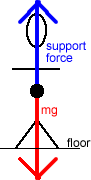
If a person is in free fall, gravity is accelerating them but they feel "weightless." |
If a person is standing on the floor, gravity is not accelerating them, but they feel "heavy." The feeling of weight is not due to gravity, the feeling of weight is due to the support force! |
|---|---|
 |
 |
However, just because you can feel accelerations doesn't mean that you always feel accelerations. For instance, when you are in free fall, you feel weightless - you feel like you are floating, not like you are accelerating (in a car, say). If you jump off a chair, you are accelerating, but you don't feel the acceleration as you fall. When astronauts take space walks from the Shuttle, they are in free fall, and they are accelerating toward the Earth, but they look and feel (I'm told) like they are floating - not falling. So, when you are a projectile, your weight, mg, is pulling you toward the Earth, and in fact your weight is accelerating you toward the Earth with acceleration "g", but you don't feel your weight - you feel like you are floating.
Right now you are seated (I assume) in front of your computer. The Earth is pulling downward on you with a force of magnitude mg, and your chair is pushing up on you with an equal support force so that the vertical net force on you is zero, and your vertical acceleration is zero - and you feel heavy. If you happen to be standing up, the floor is supplying this upward support force. If you and your chair were in free fall, your chair would not be pushing upward on you, so the net force on you would be the downward weight force, and you would be accelerating downward - but you would feel weightless. So, an interesting irony is that when only the weight force mg is pulling on you, you feel weightless. The weight force makes you heavy, but it is the upward support force - not the downward weight force - that makes you feel heavy.
So, to mimic the effects of gravity, we don't need a downward gravity-like force. We just need an upward support force of the right size! Let's apply this idea.
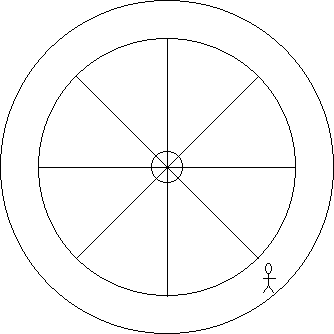First, consider a non-rotating circular space station somewhere in space. Note that the astronaut inside is floating. Since the astronaut and the space station are both in free fall, the astronaut (and everything else in the space station) feels "weightless." (See The Elevator Problem.)
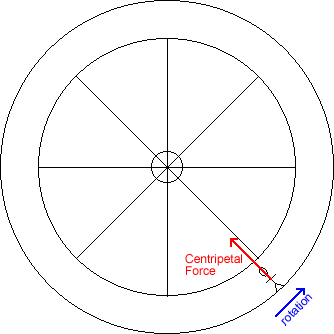In order for the astronaut to move in a circle with the space station, there must be a centripetal (center-pointing) force on the astronaut. The outside wall of the space station can supply this force. Notice that this centripetal force mimics the support force exerted by the floor on a person on Earth. Therefore, this centripetal force will make the astronaut feel heavy! There is no gravitational force - just a support force - so the astronaut isn't really heavier, she just feels heavier. All we need to do is adjust the rotational speed of the space station so that the centripetal force applied to the astronaut by the space station equals the astronaut's weight on Earth, mg, and she will feel her normal weight (but not be her normal weight!).
A capable student might reason as follows:
"For the centripetal force to mimic the feeling of weight, we want:
but this looks to me like it says that if the radius of the space station, r, increases then the velocity of the space station increases - but the book says that it decreases."
Here's the deal: In the previous calculation, v is the linear (tangential) velocity of a point on the rim of the space station, and it is absolutely true that as the radius of the space station increases - and the rotational velocity of the space station remains constant - that the linear velocity of the rim will increase.
However, it is not the linear velocity of the space station that is making the astronaut dizzy and nauseous! After all, you have a linear velocity of about 1,000 miles/hr due to the rotation of the Earth right now and that velocity does not make anyone dizzy! It is the rotational velocity that causes the problem, so let's rephrase the problem in terms of the rotational velocity.
Since 
, the equation for centripetal force becomes 
. Using this expression in the calculation above gives:
In this result, increasing the radius, r, decreases the rotational velocity - as we expect.
last update February 2, 2008 by JL Stanbrough
