Physics Lab - Work & Kinetic Energy
(uses Science WorkshopTM
Interface)
![[Up]](../../../NavIcons/Up.GIF)
![[Home]](../../../NavIcons/Home.GIF)
![[Help]](../../../NavIcons/Help.GIF)
Purpose:
The purpose of this lab is to compare the work done on an object
with the object's change in kinetic energy.
Discussion:
The Work/Energy Equation says
"The work done on an object by the net force on it equals the
object's change in kinetic energy." or, in symbols:
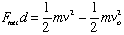
In this lab, you let gravity do work on a dynamics cart and
compare the work done on the cart to the cart's kinetic energy.
Here's how it's done.
As just mentioned, a hanging mass will be used to supply the
force, so if the mass is m, then Fnet = mg. First, you can
start the cart from rest, so that its initial kinetic energy is
zero.
You might want to try the Work
& Kinetic Energy Simulation before you do this lab. It will
give you a good idea of what quantities you need to measure and
calculate.
Equipment:
|
dynamics cart
|
string (about 1.5 meters)
|
assorted masses
|
|
weight hanger (paper clip)
|
pulley assembly for dynamics track
|
index card
|
|
Science WorkshopTM interface
|
photogate with stand
|
"Basic
Timer" experiment file
|
|
balance
|
level
|
dynamics track with bumper
|
|
tape
|
computer
|
data table
|

Setup:
- Your instructor may have already assembled the apparatus, but
if not:
- Attach the Science WorkshopTM interface
to the computer and switch the interface on.
- Attach the photogate plug to Digital Channel 1 on the
interface.
 Attach
the bumper and pulley assembly to the dynamics track as
shown.
Attach
the bumper and pulley assembly to the dynamics track as
shown.
- Open the "Simple Timer" experiment file. (Ask your instructor
where to find this file).
- Level the dynamics track using the screw(s) on the bottom of
one end.
- Attach one end of the string to the dynamics cart and the
other end to a weight hanger (which you can make out of a paper
clip). The weight hanger should be just below the pulley when the
cart is at the opposite end of the track. Measure and record the
mass of the dynamics cart, string, and weight hanger.
- Construct a "timer flag" for the dynamics cart from the index
card or stiff paper. Measure and record the width of the flag, d,
in the data table, then
attach the flag to the dynamics cart with a small piece of
tape.
- Pick and record a starting position for the cart near the
non-pulley end of the track. You might want to use a small piece
of tape to mark this position.
- Now, pick a stopping position for the cart near the pulley end
of the track. Be sure that the cart reaches the stopping position
on the track before the weights touch the floor!
 Position
the photogate on the track so that the LED on the photogate comes
on just as the dynamics cart reaches the stopping position.
Position
the photogate on the track so that the LED on the photogate comes
on just as the dynamics cart reaches the stopping position.- Place a small mass on the weight hanger Record the mass, m, in
the data table.
Note: In the data table, the
mass hanging from the weight hanger is called "Hanging mass, mh".
It is the weight of this mass that pulls the dynamics cart. The
column labeled "Added mass, ma" is where you record any
mass added to (riding on) the cart in a trial.
- Try a practice run. You need to release the cart from rest at
the starting position. The photogate LED should light just as the
cart reaches the stopping position, and you should catch the cart
before it hits the bumper.
Procedure:
- Position the cart at the starting position on the track.
- Click "Start" in the experiment window.
- Release the cart.
- Catch the cart BEFORE it hits
the bumper.
- Press "Stop" in the experiment window.
- Record the time in your data table.
- Repeat to check the consistency of your results. When you are
satisfied, change the hanging mass, or add mass to the dynamics
cart and repeat. For convenience, don't change the starting
or stopping positions.
Results:
Note about units: In this lab, it is most convenient to
measure distances in centimeters and masses in grams. Instead of
converting these to kilograms and meters, the data tables are set up
to accept the original units. This means that forces will have units
of gm cm/s2. The name for this force unit is
"dyne".
The dyne is not used as often these days as the Newton, but it is a
convenient unit for small forces. In this system, work and energy
will have units dyne cm or gm
cm2/s2, which is called an "erg".
Although the erg is not as commonly used as the Joule, it is still a
convenient unit for small energies.
For each trial. (Show a sample calculation.)
- Calculate the total mass set in motion, M = mc +
ma + mh.
- The force, F, that pulls the cart is the weight of the hanging
mass = mh. (Note: g = 980 cm/s2)
- The velocity, v, of the cart equals the width of the flag
divided by the time for the flag to pass through the photogate =
d/t.
- The work done by gravity =
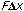 .
.
- The kinetic energy of the system =
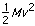 .
.
- The percent of difference between the work done on the system
and its final kinetic energy.
Conclusions:
How does the work done on a system by the net force compare to the
change in kinetic energy of the system? Why do you think so? What do
you think accounts for the discrepancies in your results?
![[Up]](../../../NavIcons/Up.GIF)
![[Home]](../../../NavIcons/Home.GIF)
![[Help]](../../../NavIcons/Help.GIF)
last update November 21, 2007 by JL
Stanbrough

 Attach
the bumper and pulley assembly to the dynamics track as
shown.
Attach
the bumper and pulley assembly to the dynamics track as
shown. Position
the photogate on the track so that the LED on the photogate comes
on just as the dynamics cart reaches the stopping position.
Position
the photogate on the track so that the LED on the photogate comes
on just as the dynamics cart reaches the stopping position.