Physics Notes - Dynamics
The Work/Energy Equation
![[Next]](../../NavIcons/Next.GIF)


The Work/Energy Equation:
The Work/Energy Equation is:
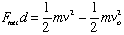
(A derivation is
available.)
So what?
Suppose we call the quantity "one-half the mass times the velocity
squared" the Kinetic Energy
of the object. Then 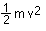 is
the final kinetic energy of the object, and
is
the final kinetic energy of the object, and 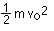 is
the starting kinetic energy of the object. If we call the quantity
"force times distance" the Work done
on the object, then
is
the starting kinetic energy of the object. If we call the quantity
"force times distance" the Work done
on the object, then 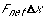 is the work done on the object by the net force. Therefore, the
previous equation says:
is the work done on the object by the net force. Therefore, the
previous equation says:
Work done by the net force = final
kinetic energy - starting kinetic energy
or:
The work done on the object by the net force =
the object's change in kinetic energy.
Very Important "Fine Print!"
- It needs to be emphasized that the work/energy equation only
applies to work done by the net force in a mechanical system - the
work done by just any old force may or may not show up as kinetic
energy, but the work done by the net force always shows up as kinetic energy.
- This version of the work-energy equation (
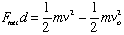 ) was derived for one-dimensional motion and is valid only if (1) the net force on the object is constant, and (2) the net force and displacement of the object are along the same line. If the situation involves two or more dimensions or if the net force is not constant, the work-energy equation is still valid, but it looks more complicated.
) was derived for one-dimensional motion and is valid only if (1) the net force on the object is constant, and (2) the net force and displacement of the object are along the same line. If the situation involves two or more dimensions or if the net force is not constant, the work-energy equation is still valid, but it looks more complicated.
- Sometimes people think that the work-energy equation (
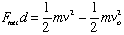 )says that the net force on an object always does work, since the left side of the equation is never zero as long as the net force and displacement aren't zero. If the net force is constant and the net force and displacement lie on the same line, this is true, but it is not true in general!
)says that the net force on an object always does work, since the left side of the equation is never zero as long as the net force and displacement aren't zero. If the net force is constant and the net force and displacement lie on the same line, this is true, but it is not true in general!
![[Next]](../../NavIcons/Next.GIF)


last update November 21, 2007 by JL
Stanbrough
is
the final kinetic energy of the object, and
is
the starting kinetic energy of the object. If we call the quantity
"force times distance" the Work done
on the object, then
![]() is the work done on the object by the net force. Therefore, the
previous equation says:
is the work done on the object by the net force. Therefore, the
previous equation says: