On a previous page, we derived the work-energy equation in one dimension as . This is perfectly valid as long as the net Force, Fnet, and the displacement,
![]() , lie along the same line and as long as the net force is constant. We know that work is not really force times distance in general. Does this mean that the Work-Energy equation is only valid in special situations? No - we just need to use a more-sophisticated version of the equation in many situations.
, lie along the same line and as long as the net force is constant. We know that work is not really force times distance in general. Does this mean that the Work-Energy equation is only valid in special situations? No - we just need to use a more-sophisticated version of the equation in many situations.
In two (or more) dimensions, we know that as long as the force on an object is constant, the work done by the force is:
where ![]() is the angle between F and
is the angle between F and ![]() . In two dimensions, then, the Work-Energy Equation becomes:
. In two dimensions, then, the Work-Energy Equation becomes:
Note the addition of the "![]() " on the left side of the equation. The Work-Energy equation still says "The work done on an object by the net force on it equals the object's change in kinetic energy.", but it is possible that the net force won't do any work!
" on the left side of the equation. The Work-Energy equation still says "The work done on an object by the net force on it equals the object's change in kinetic energy.", but it is possible that the net force won't do any work!
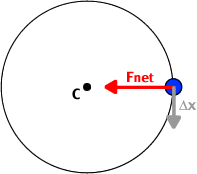 Imagine a ball attached to the end of a string being whirled in a horizontal circle with a constant speed. The net force on the ball is a centripetal force which points toward the center of the circle, and the (instantaneous) displacement
Imagine a ball attached to the end of a string being whirled in a horizontal circle with a constant speed. The net force on the ball is a centripetal force which points toward the center of the circle, and the (instantaneous) displacement ![]() is tangent to the circle, so the angle
is tangent to the circle, so the angle ![]() between the net force and the displacement is always 90o. Since cos(90o) = 0, the work done by the net force in this case is zero.
between the net force and the displacement is always 90o. Since cos(90o) = 0, the work done by the net force in this case is zero.
This does not violate the Work-Energy equation! Since the speed of the ball is constant, its kinetic energy remains constant, so the ball's change in kinetic energy is zero. Even though you exert a net force on the ball, you do zero work whirling the ball, and the ball's kinetic energy remains the same.
last update January 6, 2006 by JL Stanbrough