Elastic (Spring) Potential Energy
![[Prev]](../../NavIcons/Prev.GIF)

![[Up]](../../NavIcons/Up.GIF)
![[Home]](../../NavIcons/Home.GIF)
![[Help]](../../NavIcons/Help.GIF)
The Problem:
An elastic (Hooke's Law) force is a conservative force - it stores
energy. How much? In other words, what is the elastic potential
energy of a spring that has been stretched a distance x?
The Solution:
Following the 2-step process for
calculating potential energy in general:
- It would be convenient to pick the unstretched, at rest
position of the spring to be the EPE = 0 point.
- The elastic potential energy (EPE) at a distance x, then,
equals the negative of the work done by the Hooke's Law force as
the spring is stretched from x = 0 to its final position. Since we
know that we do work at least equal to (1/2)kx2 in
stretching the spring a distance x, the spring must do
-(1/2)kx2 work Therefore, the elastic potential energy
of the spring at point x is given by:
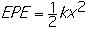
Examples:
Example 1: If the force to stretch a spring is given as F =
(100 N/m)x, then what is the potential energy of the spring if it is
stretched 2 meters from rest?
Solution: Here k = 100N/m and x = 2 m. Therefore:
EPE = (1/2)kx2 = (1/2)(100N/m)(2
m)2 = 200 Joules
Example 2: It takes a force of 20 Newtons to hold a spring
stretched to a distance of 40 cm. What is the elastic potential
energy of the spring at this position?
Solution: We know that F = 20 N when x = 40 cm = 0.40 m.
Since F = kx, then k = F/x = (20 N)/(0.40 m) = 50 N/m. Now, EPE =
(1/2)kx2 = (1/2)(50 N/m)(0.40 m)2 = 4
Joules.
![[Prev]](../../NavIcons/Prev.GIF)

![[Up]](../../NavIcons/Up.GIF)
![[Home]](../../NavIcons/Home.GIF)
![[Help]](../../NavIcons/Help.GIF)
last update December 26, 2005 by JL
Stanbrough