
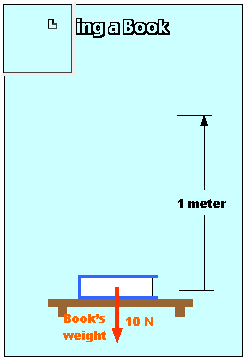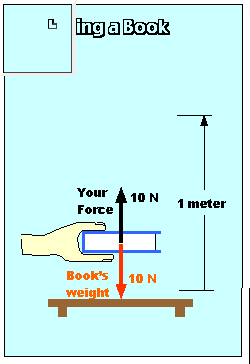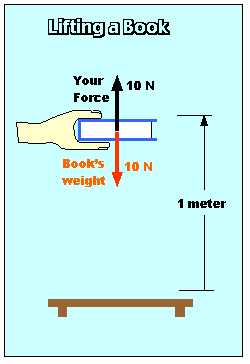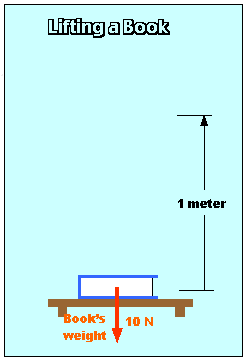
Suppose you lift a book (which weighs 10 Newtons) at constant velocity through a vertical distance of 1 meter, as shown at left.
You have to exert a force of 10 Newtons to lift the book (Newton's First Law), so the work you do is:
Workyou = Fd = (10 N)(1 m) = 10 Joules
The Work-Energy Equation might lead you to think that since you did 10 Joules of work on the book, its kinetic energy should increase by 10 Joules - but this doesn't happen. Why? Shouldn't adding 10 Joules of energy to the book increase its kinetic energy by 10 Joules? Certainly, if the force you exerted were the only force on the book, its kinetic energy would indeed have increased by 10 Joules - so what happened?
The Earth exerts a vertically-downward force on the book (its weight). Since the direction of the force is opposite to the direction of the book's displacement, the work that the Earth did on the book is:
WorkEarth-up = -Fd = (10 N)(1 m) = -10 Joules
At the same time that you were doing work on (adding energy to) the book, gravity was doing negative work on (taking energy from) the book. As you were giving the book 10 Joules of kinetic energy, the gravitational force was taking away 10 Joules of kinetic energy. The net result was that the kinetic energy of the book didn't change. But where did the energy that the gravitational force took from the book go?
When you let go of the book, it accelerates toward the Earth - because the Earth is exerting a downward net force on it. As it falls, the Earth (gravity) does work on the book:
WorkEarth-down = Fd = (10 N)(1 m) = 10 Joules
This work does increase the kinetic energy of the book - by 10 Joules (Since the weight of the book is the net force on the book in this case, the work-energy equation applies.).
Notice that, in the end, the 10 Joules of work that you originally did on the book does eventually get converted to kinetic energy of the book! It was taken from the book by the gravitational force - but it was saved or stored somehow (Contrast this with work done against friction). When you let go of the book, the book gets its kinetic energy!
