Pushing a Book

Work Done Against Friction

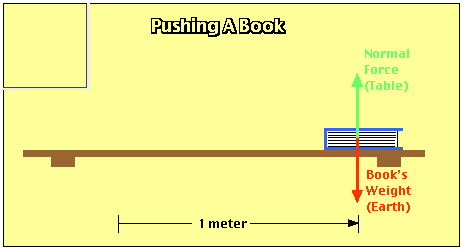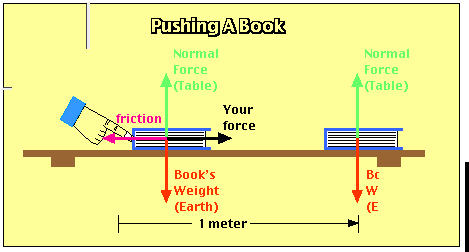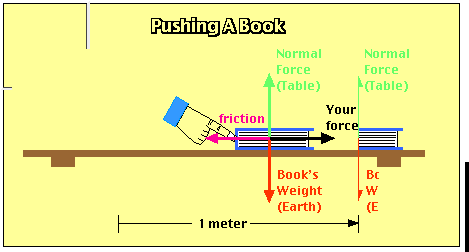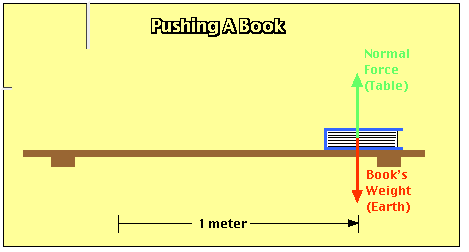
Suppose you have to exert a force of 10 Newtons to push a book 1 meter across a horizontal table at constant velocity (as shown above). Since your force is in the direction the book moves, the work you do on the book is given by:

Your work = Fx = (10 N)(1 m) = 10 Joules

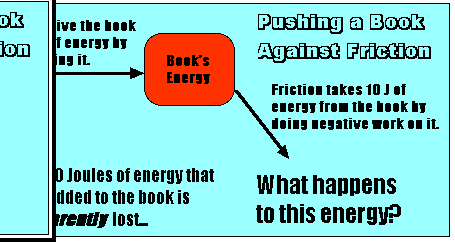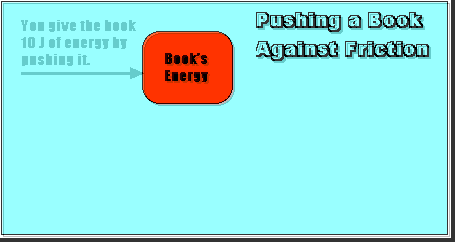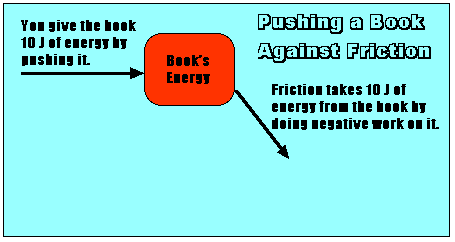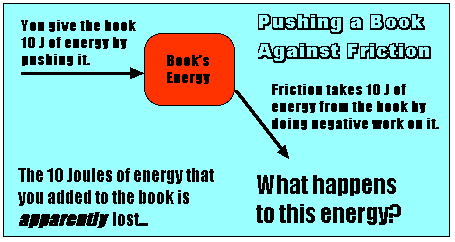
The work-energy equation would lead you to think that doing 10 Joules of work on the book should increase the kinetic energy of the book by 10 Joules - but that doesn't happen (the speed of the book is constant). What's going on?

A friction force opposes the motion of the book. This force must also be 10 Newtons (Since the book moves at constant velocity, the net force on it must be zero.). The friction force pulls in the opposite direction from the direction the book moves, the work done by friction is given by:

Work done by friction = -Fx = -(10 N)(1 m) = -10 Joules

This means that the friction force removes 10 Joules of energy from the book. So, while you were adding 10 Joules of energy to the book, friction was busy taking the 10 Joules of energy away from the book. This is why the kinetic energy of the book does not change!

What happens when you stop pushing? Nothing. The book just sits there. The 10 Joules of energy that you gave to the book is apparently gone - in contrast with what happens when you stop lifting the book.

What about work done by the gravitational force (the book's weight) and the normal force exerted by the table? Since these forces are perpendicular to the displacement of the book, they do no work on the book! (Think about it - a book lies at rest on a table. Both the weight of the book and the table's normal force act on the book - yet the book never moves! Neither of these forces can change the book's energy!)

last update November 28, 2007 by JL Stanbrough