Work to Stretch a Spring
A More-Mathematical View
![[Prev]](../../NavIcons/Prev.GIF)

![[Up]](../../NavIcons/Up.GIF)
![[Home]](../../NavIcons/Home.GIF)
![[Help]](../../NavIcons/Help.GIF)
We can generalize the method shown above to derive an equation that
gives the work done in stretching a spring a certain distance.
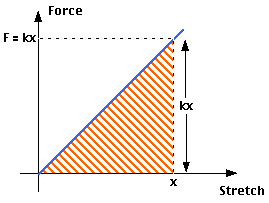 The
diagram at right shows a graph of force vs. stretch for a spring. The
blue line represents the graph of F = kx (Hooke's Law). We know that
the area shaded in red represents the
work you would need to do to stretch the spring a distance x from
its rest position.
The
diagram at right shows a graph of force vs. stretch for a spring. The
blue line represents the graph of F = kx (Hooke's Law). We know that
the area shaded in red represents the
work you would need to do to stretch the spring a distance x from
its rest position.
Since this area is a triangle, the shaded area =
(1/2)(base)(height) = (1/2)(x)(kx) = (1/2)kx2.
Therefore, the work done in stretching a spring a distance x from
its rest position is:

Examples:
Example 1: If the force to stretch a spring is given by F =
(100 N/m)x, how much work does it take to stretch the spring 4
meters from rest?
Solution: We have k = 100 N/m and x = 4 m. Therefore, Work
= (1/2)kx2 = (1/2)(100 N/m)(4 m)2 = 800
Joules
Example 2: A spring is stretched 60 cm, and it takes a force
of 40 Newtons to hold it there. How much work did it take to stretch
the spring to this point?
Solution: We know that F = 40 N when x = 60 cm = 0.60 m.
Since F = kx, k = F/x = (40 N)/(0.60 m) = 67 N/m. Now, work =
(1/2)kx2 = (1/2)(67 N/m)(0.60 m)2 = 12
Joules
last update December 11, 2003 by JL
Stanbrough
 The
diagram at right shows a graph of force vs. stretch for a spring. The
blue line represents the graph of F = kx (Hooke's Law). We know that
the area shaded in red represents the
work you would need to do to stretch the spring a distance x from
its rest position.
The
diagram at right shows a graph of force vs. stretch for a spring. The
blue line represents the graph of F = kx (Hooke's Law). We know that
the area shaded in red represents the
work you would need to do to stretch the spring a distance x from
its rest position.