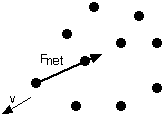
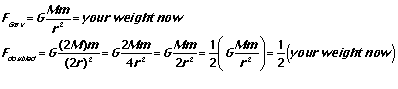Physics - Chapter 12

Assignment Answers

Ch 12 Review Answers:

  1. Newton thought that a force must act on the Moon because, since it moves in a curved (almost, but not quite) circular path, it is accelerating. After all, the direction of its velocity is constantly changing, and acceleration is the rate velocity changes. An acceleration requires a net force (2nd Law).
  2.  
  3. The Moon (and every other Earth satellite) is in free fall toward the Earth, but it is a projectile whose tangential velocity keeps it from getting closer to the Earth. In the same time that the Moon falls a centimeter, the Earth curves a centimeter out from under it!
  4.  
  5.  
  6. In order for a scientific hypothesis to advance to the status of a scientific theory, it must be thoroughly and extensively tested.
  7.  
  8.  
  9. Since Fgrav = GMm/r2, the gravitational force is directly proportional to G. The small size of the gravitational constant G tells you that the gravitational force is actually quite weak compared to other known forces like the electric, magnetic, and nuclear forces.
  10. You need to know: (1) your mass, (2) the Earth's mass, and (3) the radius of the Earth in order to determine the gravitational force on you, which is your weight.
  11. The gravitational force is an inverse-square-law force - the strength of the force decreases with the square of the distance between objects. In other words, twice the distance means one-fourth of the force, three times the distance means one-ninth of the force, etc.
  12. (a) If you were five times farther from the center of the Earth than you are now, your weight would be 1/25 ( = 1/52) of your current weight.
    (b) If you were ten times farther from the center of the Earth than you are now, your weight would be 1/100 (= 1/102) of your current weight.

Ch 12 Plug & Chug Answers:

  1. F = 9.8 N
    (Note that this is the same result you would get from w = mg.)
  2.  
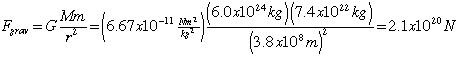
  3.  2.0 x 10^20 N
  4.  
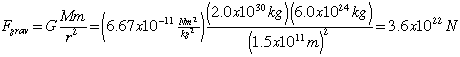
    (Comparing the answers for this question and the last one, notice that the gravitational force that the Sun exerts on the Moon is about 100 times as much as the gravitational force that the Earth exerts on the Moon. Why, then, does the Moon orbit the Earth and not the Sun? )

Ch 12 Think & Explain Answers:

  1. No, this label is not cause for alarm! The same thing can be said about every object in the universe - including you!
  2. The same amount of force. The forces "Earth pulls Moon" and "Moon pulls Earth" are a Newton's 3rd Law action/reaction pair.
  3. 500 N toward the center of the Earth. This gravitational force is the force we commonly call her weight.
  4. If the gravitational force of the Sun on the planets suddenly disappeared, they would move off with the velocity that they had at that instant (Newton's 1st Law). So, they would move in a straight line tangent to their orbit, at constant speed.
  5.  
  6. (a) Yes, if the Moon were twice as massive, the gravitational force of the Earth on the Moon would be twice as much, since the gravitational force is proportional to both masses involved.
    (b) Yes, the gravitational force that the Moon exerts on the Earth would double also (according to Newton's Third Law).
  7. A rocket going from the Earth to the Moon would require more fuel. Since the Earth has more mass than the Moon, the Earth will exert a larger gravitational force on the rocket than the Moon would (things weigh less on the Moon). This means that the rocket would have to exert a larger force to balance its weight leaving the Earth than leaving the Moon. Since the rocket exerts a larger force leaving the Earth, it must do more work to leave the Earth, which takes more energy (in the form of chemical potential energy stored in the rocket fuel).
  8. Gravitational forces on a galaxy

    Net force on a galaxy

    Gravitational forces on a galaxy near the "edge" of the Universe. (Not all forces are shown.)

    Net force on a galaxy near the "edge" of the Universe.

    The observation that the expansion of the Universe is slowing down is consistent with the law of gravity. Every object in the Universe attracts every other object in the Universe with a gravitational force. The diagram on the left above shows some of the gravitational forces on a galaxy near the "edge" of the universe. Looking at the diagram you can see that all of the forces on this galaxy point "inward", since all gravitational forces are attractive. This means that the net force on this galaxy points "inward" toward the "center" of the Universe, as shown in the diagram at right above. So, if the galaxy is moving away from the "center" of the Universe (an expanding universe), then the net force on the galaxy will act to slow the galaxy down, and the expansion of the Universe should be slowing down.
    However, recent observations (since the publication of your text) seem to indicate that the expansion of the Universe is in fact NOT slowing down - in fact, the Universe seems to be accelerating. This is contrary to the behavior that the law of gravity predicts as described above. This is an area of very heated and intense research and discussion at the moment. If the Universe's expansion is really speeding up, then there has to be some previously-undetected force that is driving it. What could that force be?

Ch 12 Think & Solve Answers

  2. If the Earth's diameter doubled and its mass also doubled, your weight would be half as much as now. Your weight is the gravitational force between you and the Earth. Doubling the mass of the Earth would double your weight, since gravitational force is directly proportional to mass, but doubling the radius (which doubles if the diameter doubles) would decrease your weight by a factor of 1/4, since gravitational force is inversely proportional to the square of the radius. Mathematically:
  3. If you were twice as far from the center of the Earth as you are now, your weight would be 1/4 of its current value (See #32).

 

last update January 16, 2007 by JL Stanbrough