Problem 1 - On the Earth:
A bowling ball falls freely (near the surface of the Earth) from rest. How far does it fall in 4 seconds, and how fast will it be going at that time?
The acceleration of the ball is g - about 10 m/s2. This means that the velocity of the ball increases by 10 m/s each second, so after 4 seconds, its velocity will increase by 10 m/s 4 times - to 40 m/s.
The instantaneous velocity of the ball increased uniformly from 0 m/s (when it was at rest) to 40 m/s, so its average velocity during its fall is half-way between 0 m/s and 40 m/s, which is 20 m/s. If you have an average velocity of 20 m/s for 4 seconds, you move 80 meters.
Since the acceleration = 10 m/s2, the speed of the ball increases by 10 m/s each second.
The ball's average speed for the first 4 seconds is the average of 0 m/s and 40 m/s, its starting and ending speeds, and distance = average speed times time.
So the object will have fallen 80 meters, and its speed will be 40 m/s.
Since the ball started from rest:
v = gt = (10 m/s2)(4s) = 40 m/s
So the object will have fallen 80 meters, and its speed will be 40 m/s.
A bowling ball falls freely from rest on a planet where g = 5 m/s2. How far does it fall in 4 seconds, and how fast will it be going at that time?
The acceleration of the ball is g for this planet - about 5 m/s2. This means that the velocity of the ball increases by 5 m/s each second, so after 4 seconds, its velocity will increase by 5 m/s 4 times - to 20 m/s.
The instantaneous velocity of the ball increased uniformly from 0 m/s (when it was at rest) to 20 m/s, so its average velocity during its fall is half-way between 0 m/s and 20 m/s, which is 10 m/s. If you have an average velocity of 10 m/s for 4 seconds, you move 40 meters.
Since the acceleration = 5 m/s2, the speed of the ball increases by 5 m/s each second.
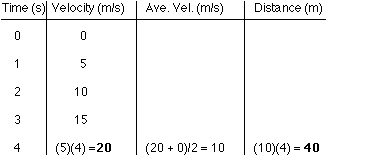
The ball's average speed for the first 4 seconds is the average of 0 m/s and 20 m/s, its starting and ending speeds, and distance = average speed times time.
So the bowling ball will have fallen 40 meters, and its speed will be 20 m/s.
Since the ball started from rest:
v = gt = (5 m/s2)(4s) = 20 m/s
So the object will have fallen 40 meters, and its speed will be 20 m/s.