BHS -> Staff -> Mr. Stanbrough -> Physics -> Mechanics -> Kinematics -> this page
Do you wonder where this equation came from? A derivation of this equation is available.
A car, initially at rest, begins to accelerate at 4.5 m/s2. How fast, in m/s, will it be going in 5.0 seconds?
Note: The steps are labeled in this solution to point out the steps involved in solving a kinematics problem. In solving an actual problem, you would generally not label step 1, step 2, etc.
Step 1 - Understand the problem.
Step 2 - Translate into physics:
vo = 0 m/s
a = 4.5 m/s2
v = ?
= 5.0 s
Step 3 - Find a kinematics equation:
The kinematics equation that relates v, vo, a, andis:
This is not necessary, since the equation is already solved for "v".
Step 5 - Substitute known values:
(Notice that a seconds unit cancels in the right-hand term to leave m/s as the unit.)
Answer: The car will be going 23 m/s in 5.0 seconds.
If the car accelerated at 4 m/s2, its velocity would change by 4 m/s each second. In 5 seconds, it would be going 20 m/s. If it accelerated at 5 m/s2, it would be going 25 m/s in 5 sec. 23 m/s seems about right.
Here is an alternate solution for this problem. It uses simpler equations, but requires more thinking.
A boat, initially moving at 20 m/s is only moving at 2.0 m/s in the same direction, 25 seconds later. Assuming that the boat's acceleration was constant, what was the boat's acceleration during this time?
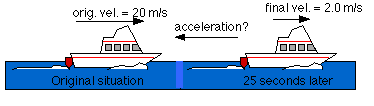
vo = 20 m/s
v = 2.0 m/s
= 25 s
a = ?
The kinematics equation that relates v, vo, a, and
is:
solving for acceleration: (What if I substitute values first, then solve?)
substituting:
Answer: The boat's acceleration is 0.72 m/s2, in the direction opposite to the boat's velocity.
Is this reasonable? Yes. If the boat had slowed by 18 m/s in 24 seconds (6 goes into both 18 and 24 evenly...), the magnitude of its acceleration would be 18/24 m/s2 = 0.75 m.s2.
Note:
In this problem, the boat slows down, or decelerates. Remember that there is no physical distinction between acceleration and deceleration - in other words, a deceleration is an acceleration. Sometimes people's misconceptions make this a sticky point. Also, don't fall into the trap of automatically making vo the smaller value, and v the bigger value. Read the problem carefully and understand what's happening before you proceed with a solution!
Also, the fact that the acceleration of the boat turned out to be negative indicates that the boat's acceleration is in the opposite direction from the boat's velocity (which is positive).
Here is an alternate solution for this example - it works quite easily.
A taxicab moving at 28 m/s applies its brakes and stops. If its brakes can decelerate it at 3.6 m/s2, how much time does it take the taxicab to stop?
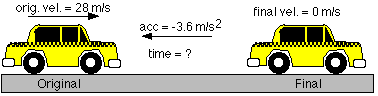
vo = 28 m/s
a = -3.6 m/s2
v = 0 m/s
= ?
The kinematics equation that relates v, vo, a, and
is:
solving for
: (What if I substitute values first, then solve?)
substituting values from the data table:
Answer: The taxicab would take 7.8 seconds to stop.
Is this a reasonable answer? If the cab's acceleration were -4 m/s2, it would lose 4 m/s of velocity each second, so it would take 7 seconds to lose 28 m/s (28/4 = 7). Yes, the answer is reasonable.
Here is an alternate solution for this problem.
A baseball has a velocity of 65 m/s downward after 8.5 seconds in free fall. What was the baseball's original velocity?
vo = ?
a = g = 9.8 m/s2 (downward)
= 8.5 s
v = 65 m/s
The kinematics equation that relates v, vo, a, and
is:
solving for vo: (What if I substitute, then solve?)
substituting values:
Answer: The baseball's original velocity was 18.3 m/s upwards. (Since the sign of the downward velocity and the downward acceleration is positive, a negative velocity must be directed upward.)
Is this reasonable? The baseball's velocity has changed by about 10 m/s (downward) each second for 8.5 seconds, so it should have changed by about 85 m/s (8.5*10) since it started. 65 m/s - 85 m/s = -20 m/s. Yes, the answer is reasonable.
Here is an alternate solution for this problem.
BHS -> Staff -> Mr. Stanbrough -> Physics -> Mechanics -> Kinematics -> this page