BHS -> Mr. Stanbrough -> -> Physics -> Mechanics -> Momentum -> Impulse & Momentum -> this page
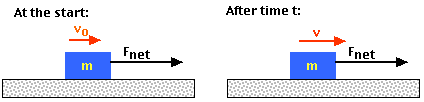
Suppose you apply a constant net force, Fnet, to an object of mass m. Newton's Second Law tells you that the object will accelerate, so if it starts with velocity vo, after some time t its velocity will be v. This situation is diagrammed below.

The acceleration of the object equals its change in velocity divided by the time it takes the velocity to change. In symbols:
Multiplying both sides of this equation by t gives:
The right side of the equation above comes from the fact that the change in velocity equals the final velocity, v, minus the starting velocity, vo. (Note: We could have just as well started with the kinematics equation v = vo + at.) This is a valid kinematical statement about the motion. To turn it into a dynamical statement about the motion, multiply both sides of the equation by the object's mass, m:
Since Newton's Second Law tells us that the net force on an object equals the product of the object's mass and acceleration, we can replace ma with Fnet in this equation. On the right side, the quantity mass times velocity is called momentum, p.
The quantity on the left, Fnett, is the impulse exerted on the object by the net force. The quantity on the right of the equation is the object's final momentum minus its starting momentum, which is its change in momentum.
This is the Impulse-Momentum Equation.
Click here for an alternate derivation.