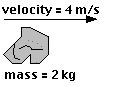
BHS -> Mr. Stanbrough -> Physics -> Mechanics -> Momentum -> this page
Suppose that a single, isolated object has no net force acting on it (either because there is nothing pushing or pulling on it, or because all of the forces that act on it cancel or balance exactly). Newton's First Law insists that the object will keep whatever velocity it currently has. Since its mass and velocity don't change, its momentum won't change either. This is true whatever the object happens to be - momentum must be conserved in any single-object system, as long as no net force acts on the system.
Of course, it a net force does act on the object, Newton's Second Law says that the object will accelerate - its velocity will change. How much? The impulse-momentum equation says that the object's change in momentum (mass times change in velocity) equals the impulse exerted on it (force times time). Does this violate the Law of Conservation of Momentum? No. The Law of Conservation of Momentum says that momentum will only be conserved if no net force (no impulse) acts on the system.
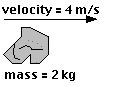
Suppose a rock is floating in space, far enough from any other matter that all forces on it can be ignored.
momentum = (mass)(velocity) = (2 kg)(4 m/s) = 8 kg m/s
If no forces act on it, the net force on the rock is zero, so Newton's First Law guarantees that the rock's velocity will not change. If its velocity and its mass don't change, its momentum must also remain the same - momentum is conserved.
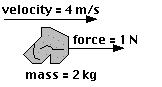 Suppose,
on the other hand, that a force of 1 Newton acts on the rock for 6
seconds. This means that there is an impulse on the rock.
Suppose,
on the other hand, that a force of 1 Newton acts on the rock for 6
seconds. This means that there is an impulse on the rock.
impulse = (force)(time) = (1 N)(6 s) = 6 Ns
From the impulse-momentum equation, we get:
impulse = change in momentum = (mass)(change in velocity)
At the end of the 5 second time interval, the velocity of the rock will have increased by 3 m/s. The momentum of the rock will be:
momentum = mv = (2 kg)(7 m/s) = 14 kg m/s