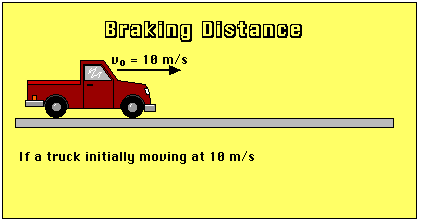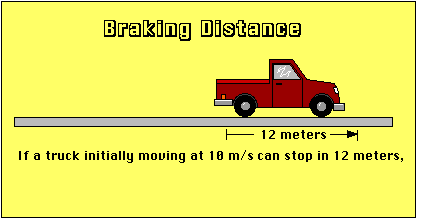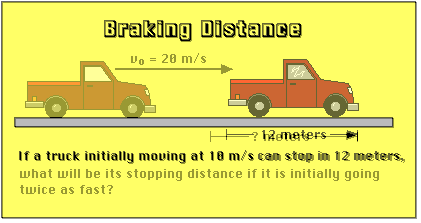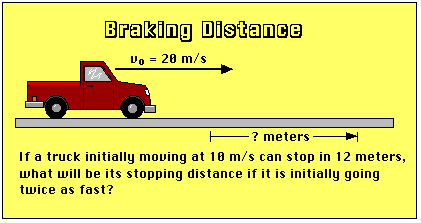

Here is some braking-distance data. You might want to compare the following solution with the work-energy approach.
If the truck starts with twice the velocity, its average velocity will be twice as much as before, since:
average velocity = (starting velocity + ending velocity)/2
Newton's Second Law says:
acceleration of the truck = (net force on the truck) / (truck's mass)
Assuming that the brakes are applied with maximum force each time, the net force on the car due to its brakes will be the same each time. The mass of the truck will stay the same - therefore the acceleration of the truck will be the same in each case. Now:
acceleration = (change in velocity) / time
Since the change in velocity will be twice as much when the truck is initially going twice as fast, the time to stop the truck must double in order that the acceleration is the same.
The distance the truck travels is given by:
distance = (average velocity)(time)
Since both the average velocity of the truck and the time to stop double, the distance to stop the truck will be four times as much (48 meters) when the truck's velocity doubles.