Relativistic Momentum

Until the twentieth century, scientists believed that the momentum of an object was a property that depends only on the amount of matter in an object -its inertia - and its velocity. Momentum = mass times velocity.

 

einstein on a bike
Prof. Einstein had slightly more momentum than mv when he was moving.

This all changed in 1905, when Albert Einstein unveiled his Special Theory of Relativity. A direct consequence of the Special Theory of Relativity is that the speed of an object cannot increase without limit. The speed of light, c, is an absolute speed limit in the universe. One would reasonably conclude, then, that there is an absolute limit on the momentum of an object, too. In 1905, Einstein said, "Not so fast, there!" According to Einstein, the momentum of an object is given by:

relativistic momentum

where m is the "rest" (zero velocity) mass, v is the velocity of the object (relative to you), and c is the speed of light (about 3.00 x 108 m/s). The table below calculates the classical (mv) momentum and relativistic momentum for a person whose rest mass is 50.0000 kg for various speeds:

 

Velocity, v

Classical Momentum

(in kg m/s)

Relativistic Momentum

(in kg m/s)
0 m/s (at rest)
0
0
3.0 m/s (walking speed)
150
150
30 m/s (about 67 mi/hr)
1 500
1 500
300 m/s (about 670 mi/hr)
15 000
15 000
3000 m/s (about 6 7000 mi/hr)
150 000
150 000
3 000 000 m/s (about 0.01c)
150 000 000
150 007 500
0.1 c
1.50 x 109
1.51 x 109
0.5 c
7.50 x 109
8.66 x 109
0.9 c
1.35 x 1010
3.10 x 1010
0.99 c
1.485 x 1010
1.05 x 1011
0.999 c
1.491 x 1010
3.35 x 1011 kg m/s
0.9999c
1.4999 x 1010
1.06 x 1012 kg m/s
Here is a graphical comparison of relativistic momentum and classical momentum. Relativistic effects are not noticeable at "normal" speeds. 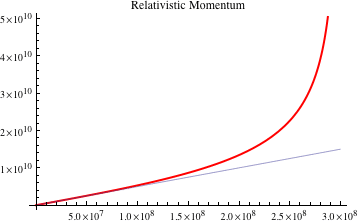momentum graph

No wonder that we don't notice this effect - even at supersonic speeds, a person's classical momentum and relativistic momentum does not differ by as much as a thousandth of a percent! You would have to be traveling at about 10 % of the speed of light before your momentum would increase by about one-half percent due to your motion...

This is certainly a very odd prediction, and it is difficult to understand why momentum would do that. Yet, experiment has shown, time and again, that this relativistic mass increase does occur. Physicists routinely accelerate subatomic particles to velocities near the speed of light, and the momentum of these particles does increase precisely in this way.

last update April 2, 2010 by JL Stanbrough