The Law of Reflection
and Curved Mirrors
![[Next]](../../NavIcons/Next.GIF)
![[Up]](../../NavIcons/Up.GIF)
![[Home]](../../NavIcons/Home.GIF)
![[Help]](../../NavIcons/Help.GIF) [Animated
version of this page]
[Animated
version of this page]
We have already established that the Law of Reflection (angle of
reflection = angle of incidence) applies to plane mirrors. If you
would place several plane mirrors into a beam of light that contained
parallel rays, you would find it relatively easy to arrange the flat
mirrors so that they would reflect their portion of the beam through
a common spot. (See the diagram at left.) If you were mathematically
inclined, you would notice that you had arranged the mirrors to
approximate a curve called a parabola. (If you were mathematically
inclined, it would be an interesting exercise to prove that this
curve is a parabola...)
As the number of plane mirrors increases in this array, the
mirrors approximate the parabola more and more closely, and the beam
focuses into a smaller and smaller area. For a perfectly-smooth
parabolic mirror, the beam will be reflected through a single point,
called the focus of the mirror.
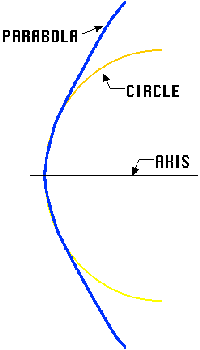 Notice
that the cross-section of this parabolic mirror is almost perfectly
circular near the center (the axis of the mirror) but "flattens out"
far from the center. This means that a parabolic mirror can be
approximated by a circular mirror as long as the objects reflected in
the mirror are small compared to the size of the mirror. This is an
important observation, since spherical (a 3D circle) mirrors are
easier and cheaper to construct that parabolic mirrors. It is also
easier to draw a circle than a parabola for a ray diagram!
Notice
that the cross-section of this parabolic mirror is almost perfectly
circular near the center (the axis of the mirror) but "flattens out"
far from the center. This means that a parabolic mirror can be
approximated by a circular mirror as long as the objects reflected in
the mirror are small compared to the size of the mirror. This is an
important observation, since spherical (a 3D circle) mirrors are
easier and cheaper to construct that parabolic mirrors. It is also
easier to draw a circle than a parabola for a ray diagram!
![[Next]](../../NavIcons/Next.GIF)
![[Up]](../../NavIcons/Up.GIF)
![[Home]](../../NavIcons/Home.GIF)
![[Help]](../../NavIcons/Help.GIF) [Animated
version of this page]
[Animated
version of this page]
last update September 20, 1999 by JL
Stanbrough