|
Since y = sin -1x is the inverse of the function y = sin x, the function y = sin-1x if and only if sin y = x. But, since y = sin x is not one-to-one, its domain must be restricted in order that y = sin-1x is a function. To get the graph of y = sin-1x, start with a graph of y = sin x. |
|
|
Restrict the domain of the function to a one-to-one
region - typically |
|
|
Reflect this graph across the line y = x to get the graph of y = sin-1x (y = arcsin x), the black curve at right. Notice that y = sin-1x has domain [-1, 1] and range |
|
| So, when you ask your calculator to graph y = sin-1x, you get the graph shown at right. (The viewing window is [-2, 2] x [-2, 2].) | 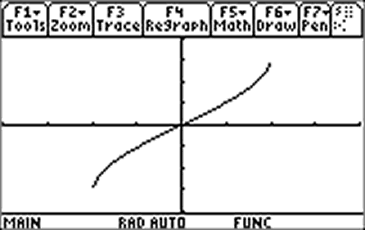 |
Most people are more familiar (and more comfortable) with the trigonometric functions than their inverses. Therefore, the first step in evaluating this expression is to say that if y = sin-1(1/2), then sin y = 1/2. This simple trigonometric function has an infinite number of solutions:
Five of these solutions are indicated by vertical lines on the graph of y = sin x below.
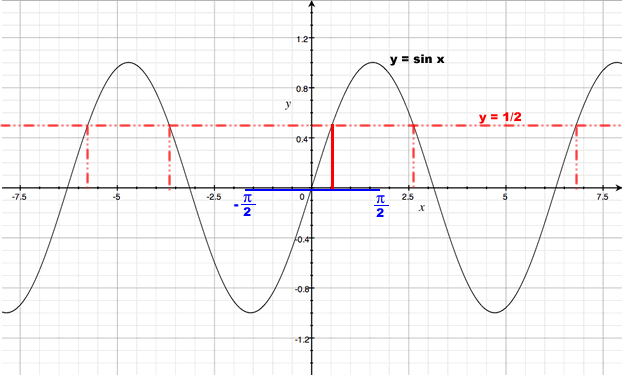
So, is the value of sin-1 (1/2) given by the expressions above? No! It is vitally important to keep in mind that the inverse sine function is a single-valued, one-to-one function. Only one of the infinite number of solutions given above is the result we want. Which one? Remember that the range of sin-1x is ![]() , which is indicated in blue in the figure above. It is really important to know the domain and range of the inverse trigonometric functions! (Why is this blue interval marked on the x-axis if it represents the range of sin-1x? Because the range of the inverse function equals the domain of the principal function.) The only solution of y = sin x that falls within the required range is
, which is indicated in blue in the figure above. It is really important to know the domain and range of the inverse trigonometric functions! (Why is this blue interval marked on the x-axis if it represents the range of sin-1x? Because the range of the inverse function equals the domain of the principal function.) The only solution of y = sin x that falls within the required range is ![]() (the solid red line in the figure above). Therefore,
(the solid red line in the figure above). Therefore,
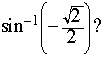
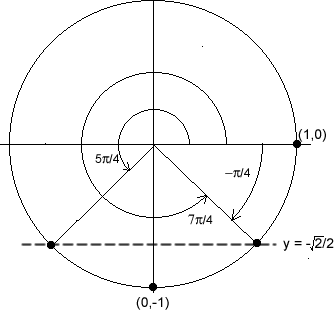
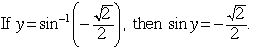 A unit-circle diagram is shown at right. Notice that candidates for the solution include:
A unit-circle diagram is shown at right. Notice that candidates for the solution include:
However, only one of these values is in the range of sin-1x (![]() ), so:
), so:
The derivative of y = sin-1 x is: (Click here for a derivation.)
The graphs of y = sin-1 x and its derivative is shown at right. The domain of y' is (-1. 1). Since y = sin-1 x is always increasing, y' > 0 for all x in its domain.
 Since
Since ![]() ,
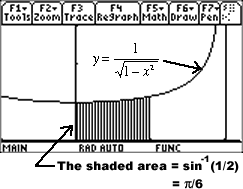
, ![]() . This means that the arcsine function arises in discussions involving integrals (and areas) of "relatively normal looking" algebraic functions. For instance:
. This means that the arcsine function arises in discussions involving integrals (and areas) of "relatively normal looking" algebraic functions. For instance:
This is the shaded area shown in the TI-89 screen shot at right. (The window is [-0.5, 1.1] x [0, 3].)