|
Date
|
Topics
|
Assignment
|
| Thu, Apr 29
B4 - 24 days - ends June 2
|
Review |
|
|
Review |
|
|
Review |
Review Assignment:
- Scan each section in Ch 12. In particular, refresh your memory on the material in the colored boxes, and read through the example problems. Then work the exercises below:
- 12-1 (p. 423) Written Exercises #1, 3
- 12-2 (p. 429) WE #9, 11
- 12-3 (p.435) WE #1, 3, 5
- 12-4 (p. 444) WE #1, 3, 5
- 12-5 (p. 450) WE #7, 9
- 12-6 (p. 455) WE #1, 9
|
|
12-7 Determinants
- What is a determinant?
- rows and columns
- size of a determinant
- Evaluating a 2x2 determinant
- Evaluating larger determinants
- minors
- the minor of an element is the determinant formed after you cross off the row and column containing that element
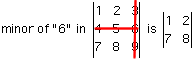 - sign of a minor
- alternates, starting with "+"
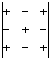
- evaluating a determinant using minors
- You can add or subtract any multiple of any row/column to any other row/column in a determinant without changing the determinant's value
|
- Read:
- 12-7 and study the examples
- Work:
- 12-7 Written Exercises #1-13
|
Wed, May 5 |
12-8 Applications of Determinants
- Cramer's Rule
- Solving 2 equations with 2 unknowns. If
ax + by = c
dx + ey = f, then
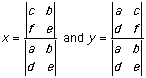
- Solving 3 equations with 3 unknowns
- Geometry
- Area of parallelogram determined by A = (xa, ya) and B = (xb, yb) is:
Area = absolute value of 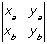
- Area of parallelepiped determined by A = (xa, ya, za), B = (xb, yb, zb) and C = (xc, yc, zc)is:
Area = absolute value of 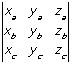
|
- Read:
- 12-8 and study the examples
- Work:
- 12-8 Written Exercises #1-17odd, 21
|
|
12-9 Determinants and Vectors in Three Dimensions
- Unit Vectors
- a unit vector is a vector whose length is 1
- Special unit vectors
- i is a unit vector in the +x direction
- j is a unit vector in the +y direction
- k is a unit vector in the +z direction
- Unit vector notation
- Cross Product
- The cross product of two vectors A x B is a vector which is perpendicular to both A and B.
- If A = (xa, ya, za) and B = (xb, yb, zb) then
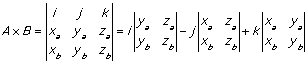
- Geometric cross product
- If
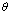 is the angle between vectors A and B, then is the angle between vectors A and B, then
|A x B| = |A||B|sin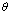
- The direction of A x B is given by the right hand rule:
"Point the fingers of your right hand in the direction of A, then curl them toward the direction of B. Your thumb points in the direction of A x B."
- Properties of the Cross Product
- A x B is perpendicular to both A and B .
- A x B = -(B x A) . This means that the vectors A x B and B x A are opposite in direction - The cross product is NOT a commutative operation!
- A x (B + C) = (A x B) + (A x C). The cross product is distributive across (vector) addition.
- |A x B| is the area of the parallelogram formed by vectors A and B.
- A x B = 0 means that A and B are parallel (and vice versa).
- Cross product and dot product on the TI-89
|
- Read:
- 12-9 and study the examples
- Work:
- 12-9 Written Exercises (p. 467) #1-9, 11-15odd
|
|
12-9 Determinants and Vectors in Three Dimensions |
- Finish the 12-9 assignment
|
|
Cellular Automata - 1 |
Assignment |
|
Cellular Automata - 2 |
|
|
Cellular Automata - 3 |
|
|
Cellular Automata - 4 |
|
Fri, May 14
(Mr. S absent)
|
Review |
- Read:
- Chapter Summary on P. 468-469
- Answer:
- Chapter Test (p. 469) #1-13
- [Hint for #10: The center of the sphere is the point (0, -1, 3), so a vector normal (perpendicular) to the plane goes through the points (0, -1, 3) and (2, -3, -2).]
|
|
Reward Day |
|
|
Review |
|
|
Test - Ch 12 & Cellular Automata
|
|
|
13-1 Arithmetic and Geometric Sequences
- Sequence
- function whose domain is usually the positive integers (natural numbers)
- first term, t1, second term t2, nth term tn
- can be specified by a formula:
tn = n2 - 1
- Arithmetic Sequences
- common difference, d = difference between any two adjacent terms
- the nth term:
- Example:
- 1, 4, 7, 10, 13, ... is an arithmetic sequence with common difference, d = 3.
- t1 = 1, t2 = 4, etc.
- the seventh term, t7 = 1 + 3(7-1) = 1 + 18 = 19
- Geometric Sequences
- common ratio, r = quotient of any two adjacent terms
- the nth term:
- Example:
- 1, 4, 16, 64, 256... is a geometric sequence with common ratio, r = 4.
- the seventh term, t7 = (1)(47-1) = 46 = 4096
|
- Read:
- 13-1 and study the examples
- Work:
- 13-1 Written Exercises (p. 476) #1-41odd
|
|
13-2 Recursive Definitions
- The formulas we used in 13-1 are called explicit definitions
- An explicit definition lets you calculate the value of any term
- A recursive definition has two parts:
- initial condition tells where the sequence starts
- recursion formula tells how to get the next term from the current term
- Finding:
- an explicit definition from a recursive definition
- Example: What is an explicit definition for the sequence t1 = 1, tn = tn-1 + 4?
- Generate some terms: 1, 5, 9, 13, 17, ...
- Recognize: This is an arithmetic sequence with t1 = 1 and d = 4.
- Since tn = t1 + d(n - 1) for an arithmetic sequence, tn = 1 + 4(n - 1), which simplifies to tn = 4n - 3.
- a recursive definition from an explicit definition
- a recursive definition from a description
- Some recursive functions
|
- Read:
- 13-2 and study the examples
- Work:
- 13-2 Written Exercises (p. 481) #1-5odd, 11-19odd, 21-25
|
|
13-3 Sums of Arithmetic and Geometric Series
- Arithmetic Series
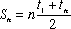 - The sum equals n times the "average term"
- Geometric Series
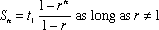 - Sn = nt1 (if r = 1)
- Calculating sums of series using a spreadsheet
|
- Read:
- 13-3 and study the examples
- Work:
- 13-3 Written Exercises (p. 489) #1-9odd, 17-23odd, 29, 31
|
|
13-4 Limits of Infinite Sequences
- In mathematics, "limit" does not mean "limitation" or "handicap" - it means "a number that the terms of the sequence get closer and closer to, or homes in on" - it is a "target."
-
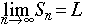 means "As the number of terms gets larger and larger, the value of the terms of sequence S get closer and closer to (or homes in on) L" means "As the number of terms gets larger and larger, the value of the terms of sequence S get closer and closer to (or homes in on) L"
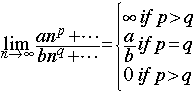 - limits that "do not exist"
|
- Read:
- 13-4 and study the examples
- Work:
- 13-4 Written Exercises (p. 496) #1-6, 9 (ans: 0), 10, 13, 15, 19, 20, 26
|
|
Quiz - Chapter 13 |
|
Thu, May 27
(Last day for seniors with privileges)
|
|
- Seniors
- turn in books
- last day to turn in assignments
|
Fri, May 28
(Senior grades due 8 A.M.)
|
No Seniors (who still have senior privileges) |
Goodbye Seniors and Best Wishes
|
|
Memorial Day - No School |
|
|
|
|
Wed, June 2
End of B4 - 23 days |
|
Have a GREAT summer break! |