Before the Engine Fires:
Let's take our system as "rocket + fuel". For simplicity, suppose that the rocket is at rest, somewhere in space, where no outside forces will exert impulses on our system. Therefore, "rocket plus fuel" is an isolated system and the Law of Conservation of Momentum applies. Since both the rocket and the fuel are at rest, their individual momenta are zero, and so the total momentum of the system is zero.
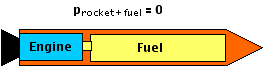
After the Engine Fires:
When the rocket's engine fires, it pushes fuel out of the end of the rocket. Suddenly, part of the fuel has momentum, mv, toward the left as shown in the diagram.
Since the total momentum of the system was zero before the rocket fired, it must still be zero. This means that the rocket must have an equal momentum to the right:
procket = -pfuel
The negative sign means that the two momentum vectors are in opposite directions (and therefore cancel). Even though the momentum of the rocket and the momentum of the fuel are the same size, their velocities are not the same size. Since the fuel has a small mass, it gets a larger velocity. Since the rocket has a large mass, it gets a smaller velocity.
Mrocketvrocket = -mfuelVfuel
